データ利活用①

データ利活用

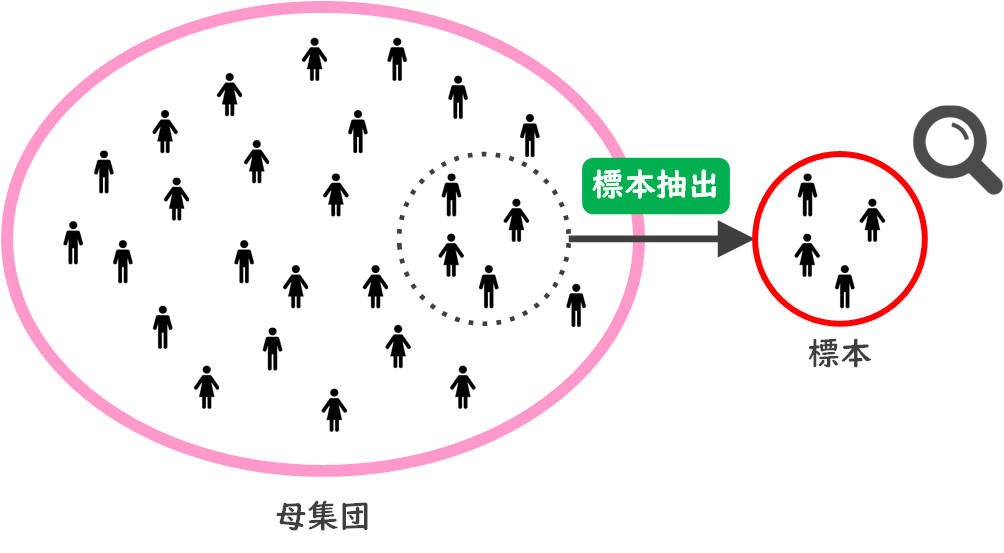
統計における母集団とは、調査や分析の対象となる全てのデータや個体の集まりを指します。

しかし、母集団全体を調査することは、コストや時間などの制約から困難な場合が多いです。そこで、標本抽出というプロセスを用いて母集団から代表的な一部分を選び出し、この標本に基づいて分析を行います。

この方法により、標本の結果から母集団全体の性質や傾向を推測することができます。

標本抽出にはいくつかの方法がありますが、主に単純無作為抽出とクラスター抽出法があります。

単純無作為抽出は、母集団の中からランダムに標本を選ぶ方法です。

この方法では、母集団の各要素が選ばれる確率が等しく、偏りのない標本を得ることができます。

これにより、標本が母集団全体を代表するものとして扱われ、推定結果の信頼性が高まります。

クラスター抽出法は、母集団をいくつかのグループ（クラスター）に分けた後、いくつかのクラスターを無作為に選び、その中のすべての要素を調査対象とする方法です。

例えば、地理的に広範囲に分布する母集団を効率的に調査する際に用いられます。

クラスター抽出法では、クラスター内の要素が似た特徴を持つことを利用して、調査対象を絞り込むことができます。

単純無作為抽出とクラスター抽出法のどちらの方法を選ぶかは、調査の目的や母集団の性質によって異なります。適切な標本抽出方法を用いることで、効率的かつ正確な統計分析が実現できます。

仮説検定は、統計学で使われる手法で、ある主張（仮説）が正しいかどうかをデータを使って評価します。

具体的には、2つの仮説、帰無きむ仮説（仮説などそもそも無かったことを表す元の仮説）と対立仮説（元の仮説と反対の仮説で、成り立つかどうか知りたい仮説）を用意し、データを調べることで、どちらの仮説が正しいかを判断しようとします。

例えば、ある学校で「この学校の生徒の平均身長は全国平均と異なる」という主張を検証したいとします。これを検証するために、以下の2つの仮説を設定します。

次に、この学校の生徒から無作為に一部を選び（標本抽出）、その平均身長を計算します。その結果をもとに、帰無仮説が正しいか、対立仮説が正しいかを判断します。もし計算した平均身長が全国平均から大きく離れているなら、帰無仮説を棄却し、対立仮説を受け入れます。

ただし、実際のデータを使って判断するため、誤りが発生する可能性があります。

帰無仮説が真であるのに誤って棄却することを第1種の誤り、対立仮説が真であるのに誤って棄却することを第2種の誤りと言います。

これらの誤りを考慮しながら、適切な判断を行うことが重要です。

A/Bテスト

A/Bテストは、ウェブサイトやアプリなどのデザインや機能を改善するための統計的手法です。

2つの異なるバージョン（AとB）を用意し、同時に一部のユーザーに表示させて、どちらが目標とする指標（クリック率、コンバージョン率など）に対して優れた結果を示すかを比較します。

この手法により、最適なデザインや機能を効果的に決定できます。

帰納推論と演繹推論

帰納推論と演繹推論は、どちらも論理的な推論の方法ですが、異なるアプローチを取ります。

帰納推論は、特定の事例から一般的な法則を導く方法です。例えば、5日連続で雨が降ったので、「この季節は雨が多い」と結論付けるのが帰納推論です。ただし、帰納推論は特定の事例に基づいているため、全ての事例に当てはまるかどうかは確実ではありません。

一方、演繹推論は、既知の法則から特定の事例に関する結論を導く方法です。例えば、「すべての人は死ぬ」から、「ある人物もいつか死ぬ」と結論付けるのが演繹推論です。演繹推論は既知の法則が正しいと仮定すれば、結論も正しいことが保証されます。

これらの推論方法は、それぞれ異なる状況や問題解決に役立ちます。帰納推論は新しい法則や原則を発見するのに役立ち、演繹推論は既知の法則や原則から特定の事例に関する結論を導き出すのに適しています。

クロスセクションデータ

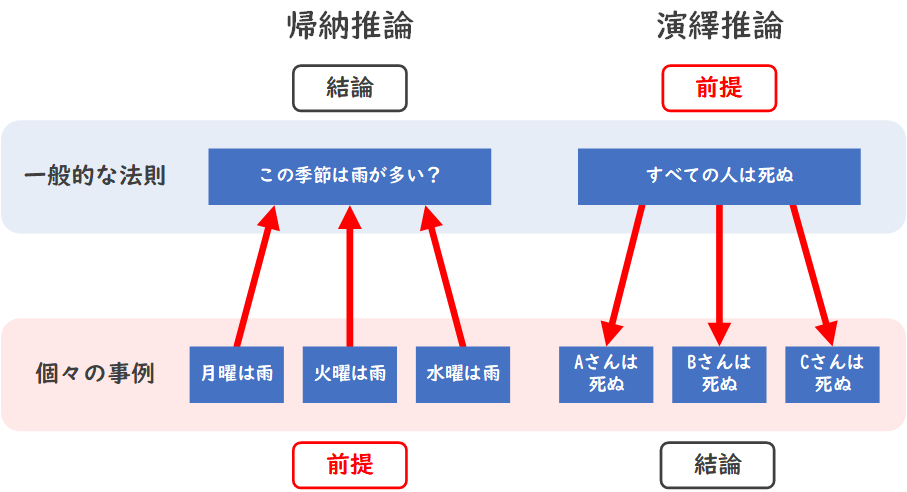
クロスセクションデータとは、ある特定の時点における場所・グループ別などに記録した複数の項目を集めたデータのことです。同一時点での複数項目間の分析ができます。

例えば、ある年の全国の市区町村ごとの人口、世帯数、出生率や、ある学期のクラスごとの英語、数学、国語の期末試験の平均点数などがクロスセクションデータになります。

このようなデータを用いて分析することで、個々のデータだけでは分からなかった全体の傾向や関係性を把握することができます。

※クロスセクション（cross-section）とは、「断面の」「横断面の」「輪切りにされた」などの意味のある英単語です。