アルゴリズム
アルゴリズムとは、問題を解決するための具体的な手順や方法のことを指します。
この手順を順番に実行することで、与えられた問題を効率的に解決することを目指します。プログラミングにおいては、アルゴリズムはコードの形に落とし込まれ、コンピューターによって実行されます。
アルゴリズムはデータのソートや検索、数値の計算、グラフの解析など、さまざまな問題に適用されます。
アルゴリズムでは特に問題を解決する効率に重点が置かれており、同じ問題を解決するための複数のアルゴリズムが存在することがあります。これらのアルゴリズムは、時間やメモリ使用量などの観点から比較され、最も効率的なものが選ばれることが一般的です。
アルゴリズムを理解することは、プログラミングやコンピューターサイエンスにおいて重要なスキルです。効率的なアルゴリズムを選択・実装することで、パフォーマンスの向上やリソースの節約が期待できます。
また、アルゴリズムを学ぶことで、論理的思考や問題解決能力が鍛えられ、プログラミングスキルが向上します。
フローチャート(流れ図)
フローチャートは、アルゴリズムの処理手順を視覚的に表現するために使われる図解法の一つで、様々な図形を使って手順を表現することができます。
フローチャートはアルゴリズムを理解しやすくするために使われ、プログラミングやビジネスプロセスの分析や設計に広く使われています。
以下は、フローチャートの図形の一覧です。
| 端子 |  | プロセスの開始や終了を示します。 |
| 処理 |  | 一つのタスクや手順を示します。 |
| 判断 | 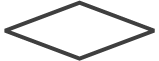 | 条件判定や選択肢を示します。通常、Yes/NoやTrue/Falseのような2つの方向に分岐します。 |
| ループ端 | 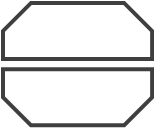 | ループの開始や終了を示します。 |
| 流れ線 | フローチャートの各要素間の流れや方向を示します。 |
アルゴリズムの基本構造
アルゴリズムの基本構造は、順次構造、選択構造、繰り返し構造の3つに分類されます。
これらの構造は、プログラムやアルゴリズムがどのように動作するかを理解するための基本的な要素です。
順次構造
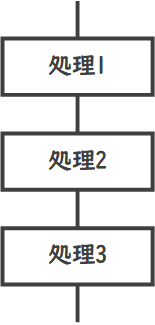
順次構造は、アルゴリズムの手順が一つずつ順番に実行される構造です。
プログラムの中で最も基本的な構造であり、手順が上から下へと進んでいくことを示します。
例えば、レシピの手順を順番に実行するのが順次構造です。
選択構造
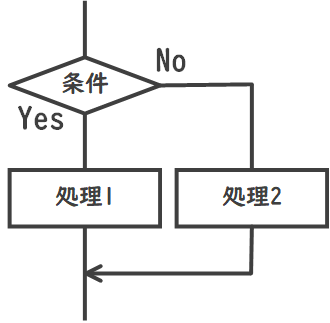
選択構造は、条件に応じてアルゴリズムの手順が分岐する構造です。
これにより、特定の条件が満たされた場合に限り、特定の手順を実行することができます。
例えば、天気が晴れている場合は外で遊び、雨が降っている場合は家で過ごす、というような選択を行います。
繰返し構造
繰り返し構造は、特定の条件が満たされるまで、アルゴリズムの手順を繰り返し実行する構造です。
これにより、同じ手順を何度も実行したり、一定の条件下でループを繰り返したりすることができます。
例えば、指定された回数だけジャンプを繰り返す、あるいはゴールにたどり着くまで歩き続ける、といった繰り返しを行います。
また、繰り返しには、処理をする前に繰り返すかどうかを判定する前判定繰返しと、処理を行った後に繰り返すかどうかを判定する後判定繰返しの2種類があります。このため、フローチャートの書き方も2種類存在します。
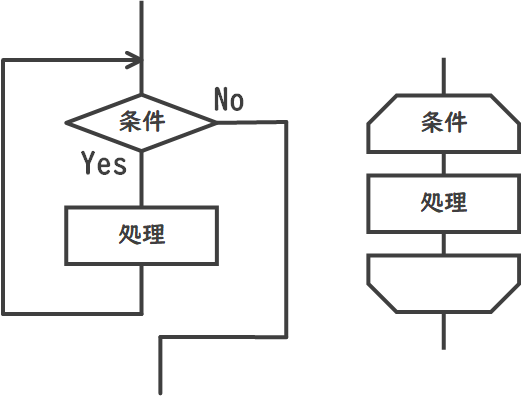
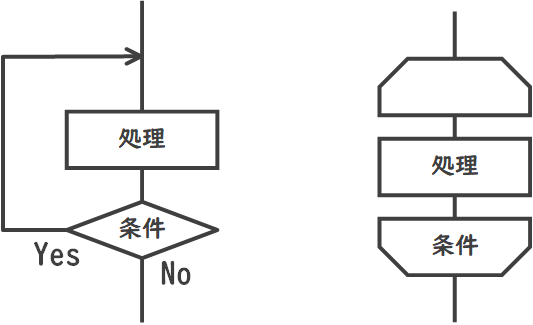
これらの基本構造は、組み合わせることでさまざまなアルゴリズムやプログラムを構築できます。
順次構造を基本として、選択構造や繰り返し構造を適切に使い分けることで、効率的で柔軟なアルゴリズムを実現できます。
変数
変数は、プログラミングにおいてデータを保持するための仕組みです。
プログラムの実行中に必要な情報を一時的に保管する場所として使われます。
変数には名前が付けられ、その名前を使ってデータにアクセスしたり操作したりできます。これにより、プログラムのコードが読みやすくなり、データを効率的に扱うことができます。
変数には以下のような要素があります。
| 変数名 | 変数にアクセスするために使用される名前です。 通常、変数名はその変数が保持するデータの目的や内容を表す名前が付けられます。 例えば、年齢を保持する変数なら「age」、名前を保持する変数なら「name」といった具合です。 |
| データ型 | 変数が保持するデータの種類を指定します。 整数(int)、浮動小数点数(float/double)、文字列(string)、ブール値(bool)などが一般的なデータ型です。 プログラミング言語によっては、明示的にデータ型を指定する必要がある場合もあります。 |
| 値 | 変数が実際に保持しているデータです。 プログラムの実行中に、変数の値を取得したり、新しい値を代入したりすることができます。 変数の値は、同じデータ型の別の値に変更することができます。変更すると、以前の値は上書きされて消去されます。 |
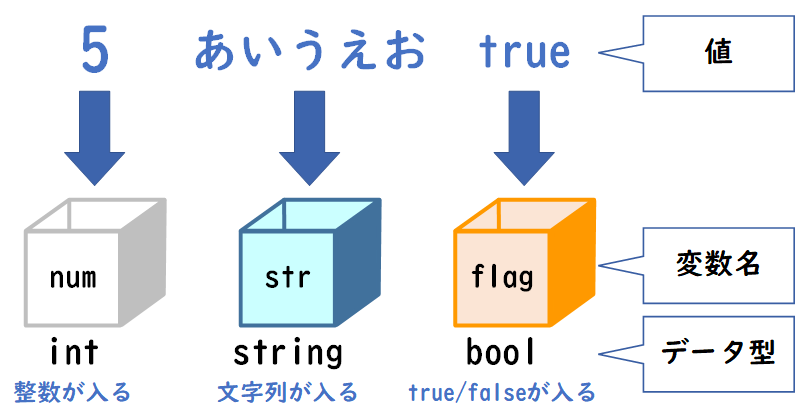
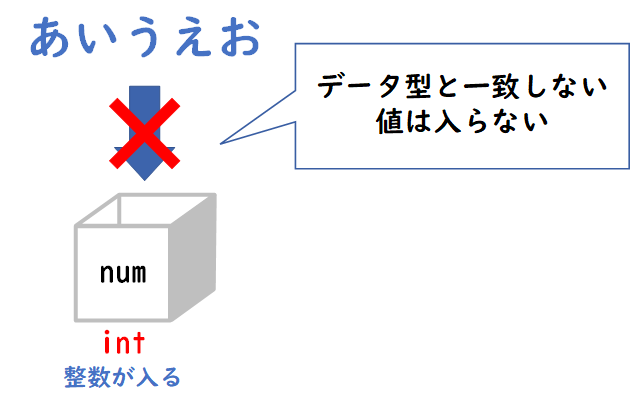
これらの要素を考慮して、変数を適切に定義・使用することで、プログラムのデータを効率的に管理し、コードの可読性や保守性を向上させることができます。
変数を使いこなすことで、プログラムの処理が簡潔になり、複雑な問題に対処しやすくなります。
変数の使用例
例えば、あるプログラムで数値の加算を行う場合、2つの数値を変数に格納してから、それらの和を計算し、結果を別の変数に格納することができます。
num1 = 5
num2 = 10
sum = num1 + num2
print(sum)この例では、num1 と num2 という2つの変数が整数値を保持し、sum という変数が2つの数値の和を保持します。そして、最後に sum の数値、つまり15という数を画面上に表示します。
変数を使用することで、プログラムの各段階でのデータを明確に表現することができ、コードが読みやすくなります。
変数は、プログラミング言語の基本的な概念であり、データの操作や処理に欠かせない要素です。
変数を理解するために、箱を使った例え話を考えてみましょう。
想像してみてください。あなたは家で整理整頓をしています。たくさんのものがあり、それらを整理するために箱を用意し、それぞれにラベルを貼りました。
例えば、「ペン」、「おもちゃ」、「本」などといったラベルです。このラベルが変数の名前に相当します。この箱に、それぞれの品物を入れていくことで、整理整頓が進んでいきます。
変数も同様に、プログラムの中でデータを整理整頓する役割を果たしています。変数は、特定のデータに名前(ラベル)を付けて、そのデータを保持する「箱」のようなものです。プログラムの中で、変数にデータを入れたり、データを取り出したり、別の変数にデータを移したりすることができます。
例えば、変数「年齢」に「20」を代入することは、年齢というラベルのついた箱に20という数字を入れることに相当します。このように、変数を使うことで、プログラムの中でデータを管理しやすくなります。また、変数の値を変更することで、プログラムの振る舞いを柔軟に変えることができます。
アルゴリズムの例
ここでは、フローチャートを使って簡単なアルゴリズムの例を挙げます。
1から10までの数を合計
以下は、1から10までの数を合計するという簡単なアルゴリズムです。

- 端子
- 「開始」
- 処理
- 変数 sum を 0 に初期化する。
- 変数 i を 1 に初期化する。
- ループ端
- i が 10 以下か判定する。10より大きければステップ6の「終了」へ
- 処理
- sum に i を加える。
- i の値に 1 を加える。
- ループ端
- ステップ3へ
- 端子
- 「終了」
簡単に言えば、このアルゴリズムは1から10までの数を加算するためのものです。
変数 i は加算のためのカウンタとして使われ、各ステップで値が増加します。値が10を超えたら、ループを終了し、プロセスが終了します。
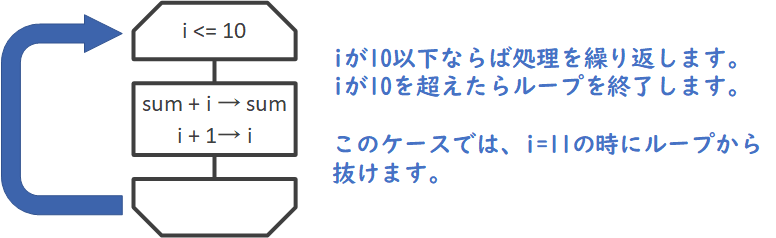
ここで、アルゴリズムの流れを追って、変数の変化を確認することトレースといいます。トレースを行うことで、アルゴリズムの各ステップでの変数の状態を明確に把握することができます。
また、ITパスポート試験の問題を解く上でも重要な手がかりとなります。
以下は、上のフローチャートをトレースしたものです。
| 状態 | 処理内容 | sumの値 | iの値 |
|---|---|---|---|
| 初期状態 | アルゴリズム開始 & sum、iの初期化 | 0 | 1 |
| ループ1回目終了時 | 0に1を足す | 1 | 2 |
| ループ2回目終了時 | 1に2を足す | 3 | 3 |
| ループ3回目終了時 | 3に3を足す | 6 | 4 |
| ループ4回目終了時 | 6に4を足す | 10 | 5 |
| ループ5回目終了時 | 10に5を足す | 15 | 6 |
| ループ6回目終了時 | 15に6を足す | 21 | 7 |
| ループ7回目終了時 | 21に7を足す | 28 | 8 |
| ループ8回目終了時 | 28に8を足す | 36 | 9 |
| ループ9回目終了時 | 36に9を足す | 45 | 10 |
| ループ10回目終了時 | 45に10を足す | 55 | 11 |
| アルゴリズム終了 | i <= 10の判定でループから出る & 終了 | 55 | 11 |
1から10までの偶数を合計
1から10までの偶数を合計するアルゴリズムを考えます。
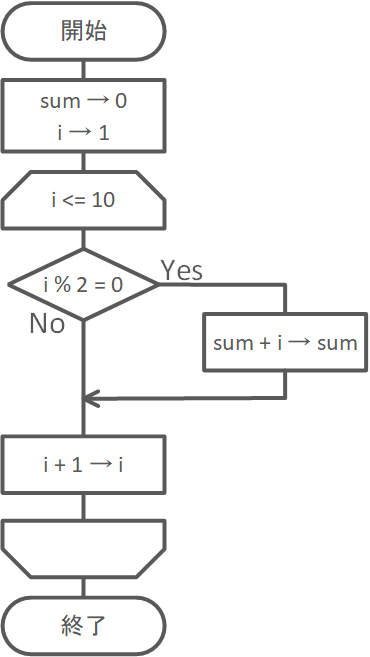
- 端子 : アルゴリズムの開始
- 処理 :
- 変数 sum を 0 に初期化する。
- 変数 i を 1 に初期化する。
- ループ端 : ここからループが始まります。
i <= 10 かどうかを判定。- Yesの場合、次に進む。
- Noの場合、ループを抜けて後の処理に進む。(ステップ8)
- 判断 : i % 2を計算することでiが偶数かどうかを確認。
- Yesの場合、5の処理に進む。
- Noの場合、6の処理に進む。
- 処理 : 偶数の場合、sum = sum + i として、iを合計に加える。
- 処理 : i = i + 1 として、iの値を増加させる。
- ループ端 : ステップ3へ戻る
- 端子 : アルゴリズムの終了
トレースの結果は以下のようになります。
| ステップ | 処理内容 | sumの値 | iの値 |
|---|---|---|---|
| 初期状態 | アルゴリズム開始 & 合計、iの初期化 | 0 | 1 |
| ループ1回目終了時 | i=1 (偶数ではないので、合計せず) | 0 | 2 |
| ループ2回目終了時 | i=2 (偶数なので、2を合計) | 2 | 3 |
| ループ3回目終了時 | i=3 (偶数ではないので、合計せず) | 2 | 4 |
| ループ4回目終了時 | i=4 (偶数なので、4を合計) | 6 | 5 |
| ループ5回目終了時 | i=5 (偶数ではないので、合計せず) | 6 | 6 |
| ループ6回目終了時 | i=6 (偶数なので、6を合計) | 12 | 7 |
| ループ7回目終了時 | i=7 (偶数ではないので、合計せず) | 12 | 8 |
| ループ8回目終了時 | i=8 (偶数なので、8を合計) | 20 | 9 |
| ループ9回目終了時 | i=9 (偶数ではないので、合計せず) | 20 | 10 |
| ループ10回目終了時 | i=10 (偶数なので、10を合計) | 30 | 11 |
| アルゴリズム終了 | i <= 10の判断でループから出る & 終了 | 30 | 11 |
