業務分析②

業務分析手法②

散布図

散布図は、2つの変数間の関係を視覚的に表現するグラフです。

各データポイントがグラフ上に点としてプロットされ、これらの点の分布を通じて変数間の相関関係を視覚的に把握できます。散布図には、正の相関、負の相関、相関無しという3つの主なパターンがあります。

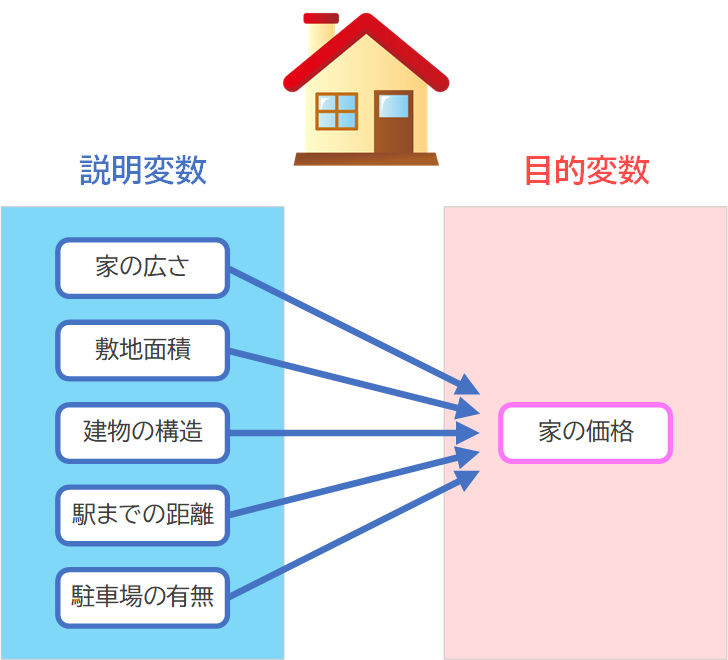
正の相関：データ点が右上がりの傾向を示す場合、2つの変数は正の相関があると言われます。これは、一方の変数が増加すると、もう一方の変数も増加することを意味します。
負の相関：データ点が右下がりの傾向を示す場合、2つの変数は負の相関があると言われます。これは、一方の変数が増加すると、もう一方の変数は減少することを意味します。
相関無し：データ点が特定の傾向を示さず、ランダムに散らばっている場合、2つの変数には相関が無いと言われます。これは、一方の変数の変化がもう一方の変数の変化に関連していないことを意味します。

散布図を使って、変数間の相関関係を視覚的に把握することができます。この情報は、データの傾向を理解したり、予測モデルを構築する際に役立ちます。

相関関数

相関関数は、2つの変数間の相関の強さや方向を数値で表す指標です。

一般的にはピアソンの相関係数が用いられます。

相関関数の値は-1から1の範囲で、1に近いほど正の相関が強く、-1に近いほど負の相関が強いとされます。0に近い場合、相関がほとんど無いことを示します。

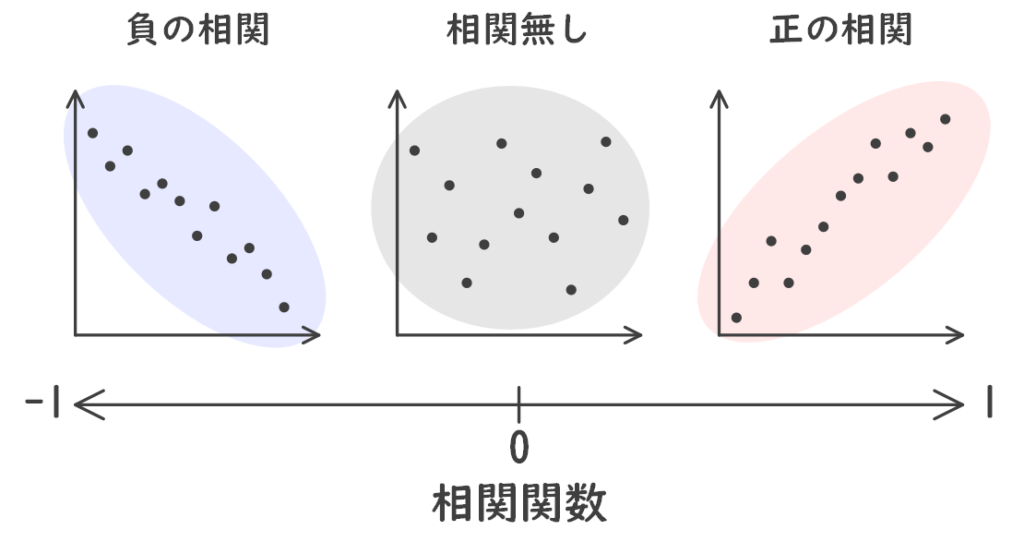
説明変数と目的変数

散布図の2つの変数のうち、説明変数は、他の変数に影響を与えると考えられる変数で、原因を表す値です。

一方、目的変数は、説明変数の影響を受けると考えられる変数で、結果を表す値です。

一般的に横軸（X軸）に説明変数を、縦軸（Y軸）に目的変数を配置します。

例えば、家の価格を予測するモデルを作成する場合、目的変数は家の価格になります。説明変数は、家の価格に影響を与えると考えられる要素、たとえば家の広さ、築年数、近くの交通機関などになります。

データ解析を通じて、説明変数と目的変数の関係を明らかにし、新しいデータに対して目的変数を予測することができます。

回帰分析

回帰分析は、説明変数と目的変数の関係性を解き明かす統計手法です。

説明変数によって、目的変数がどのように変化するかを調べます。家の広さと家賃の関係、睡眠時間とテストの点数の相関関係など、さまざまな場面で活用できます。

具体的には、以下の3つの種類に分類されます。

線形回帰分析: 説明変数と目的変数が直線関係（一次式で近似できる関係）にある場合。家の広さと家賃の関係などを分析するのに適しています。
ロジスティック回帰分析: 目的変数が2つのカテゴリ（例えば、合格/不合格）である場合。合格可能性を予測するのに適しています。
重回帰分析: 複数の説明変数を持つ場合。例えば、勉強時間、睡眠時間、朝食の有無とテストの点数の関係や、気温、曜日、祝日かどうか、周辺イベントの有無とコンビニエンスストアの1日の売上高の関係など、複数の要因が影響する関係性を分析するのに適しています。

主成分分析

主成分分析は、統計学におけるデータ解析手法の一つで、多くの量的な説明変数を、より少数の指標や合成変数（複数の変数が組み合わさったもの）にまとめる方法です。

このまとめ方は、「次元削減」とも呼ばれます。まとめた合成変数は「主成分」と称されます。

例えば、身長と体重という2次元データを、BMI（ボディマス指数）という1次元の指標に要約することで、肥満度を表現できます。

主成分分析の例

主成分分析は、多次元データを簡略化する手法です。

例えば、家の価格を予測する際に、家の広さ、築年数、部屋の数、駅までの距離、駐車場の有無など多くの要素を考慮するとします。

これらの要素は多次元のデータとなり、複雑で扱いにくいことがあります。

主成分分析を使うと、これらの多次元データを少数の主成分に変換し、データの重要な部分を保持しつつ、より簡単に分析できるようにします。

例えば、家の広さと部屋の数をまとめて「全体の大きさ」、駅までの距離と駐車場の有無をまとめて「交通の便利さ」とすることで、モデルのシンプル化と予測精度の向上を図ることができます。

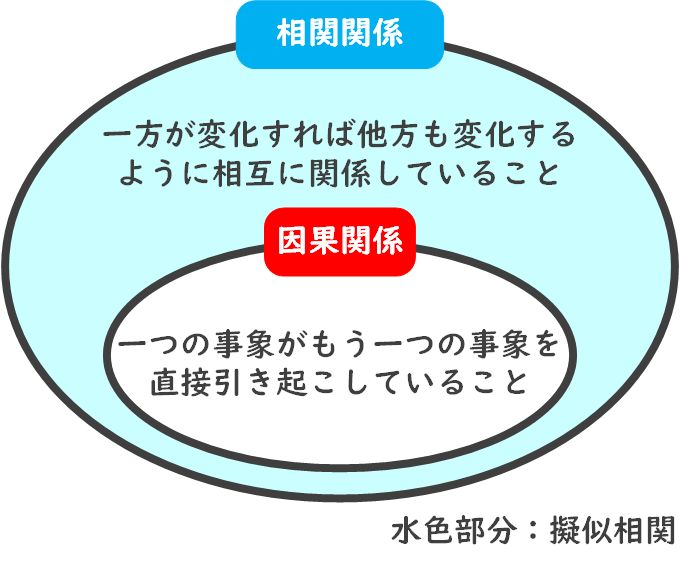
相関関係と因果関係

相関関係と因果関係は、2つの事象の間のつながりを表す考え方ですが、意味する内容は異なります。

相関関係

相関関係とは、2つの変数間に関連性があることを示します。

つまり、ある変数の値が変わると、もう一方の変数の値もそれに伴って変わる傾向があるということです。

例えば、気温が上がると、アイスクリームの売り上げも増える場合、気温とアイスクリームの売り上げは相関関係にあると言えます。

因果関係

次に、因果関係とは、ある変数がもう一方の変数に対して直接的な影響を与える関係を指します。

つまり、原因と結果の関係が存在することです。例えば、広告宣伝費を増やすと、商品の売り上げが増える場合、広告宣伝費と商品の売り上げは因果関係にあると言えます。

ただし、相関関係があるからといって、必ずしも因果関係が成立するわけではありません。2つの変数が関連しているだけで、一方が他方の原因となっているとは限らないのです。

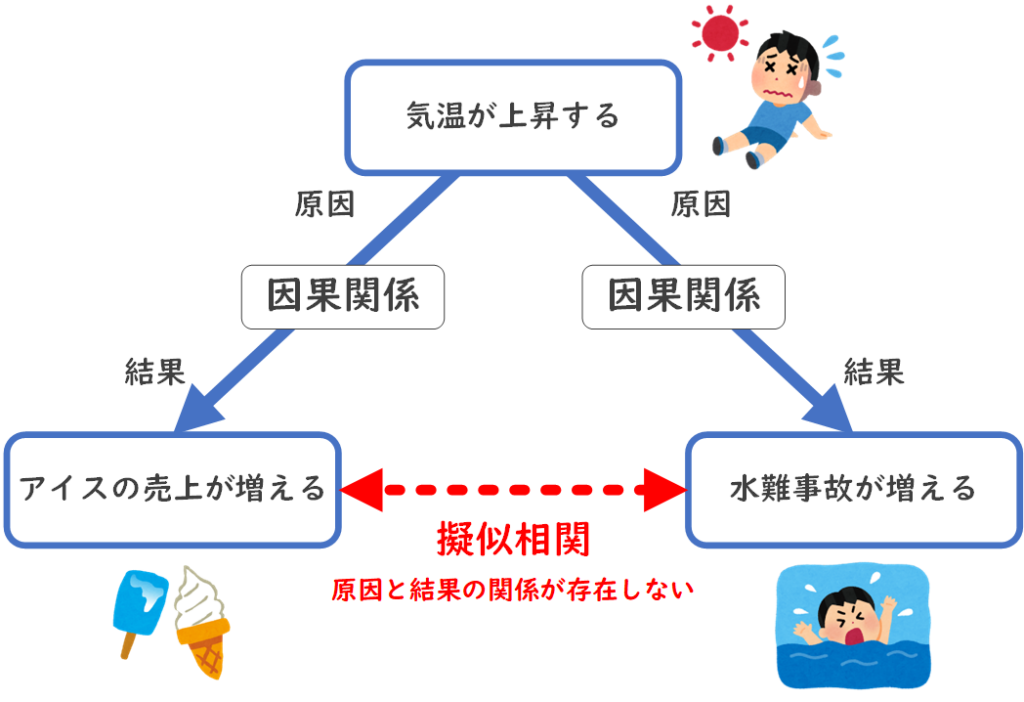
このことを説明する際によく用いられるのが、擬似相関という概念です。擬似相関とは、2つの変数間に相関関係があるように見えるが、実際には第三の変数が影響を与えているために生じる、偽の相関関係のことです。

例えば、夏になるとアイスクリームの売り上げが増え、同時に水難事故が増えることが観察される場合、アイスクリームの売り上げと水難事故は相関関係にあるように見えます。

しかし、実際には気温が高くなることが、アイスクリームの売り上げ増加と水難事故増加の共通の原因であり、アイスクリームの売り上げと水難事故には直接的な因果関係は存在しません。

このような場合、アイスクリームの売り上げと水難事故には擬似相関が発生していると言われます。

統計分析を行う際には、相関関係と因果関係を混同しないよう注意が必要です。

また、擬似相関を見極めることで、正確な分析結果や有益な情報を得ることができるようになります。実際に因果関係があるのかどうか、さらなる調査や実験が必要になることもあります。

相関関係と因果関係のまとめ

相関関係と因果関係の両方が存在する場合: 二つの変数や事象が互いに関連しており、さらに一方の変数や事象がもう一方を引き起こす関係にあるとき、これを因果関係と言います。
相関関係はあるが、因果関係はない場合: 二つの変数や事象が関連しているように見えるが、実際には一方がもう一方を引き起こしているわけではない場合、この関連性を擬似相関と言います。

したがって、相関関係があることと因果関係があることは異なるので、それぞれを正確に識別することが重要です。

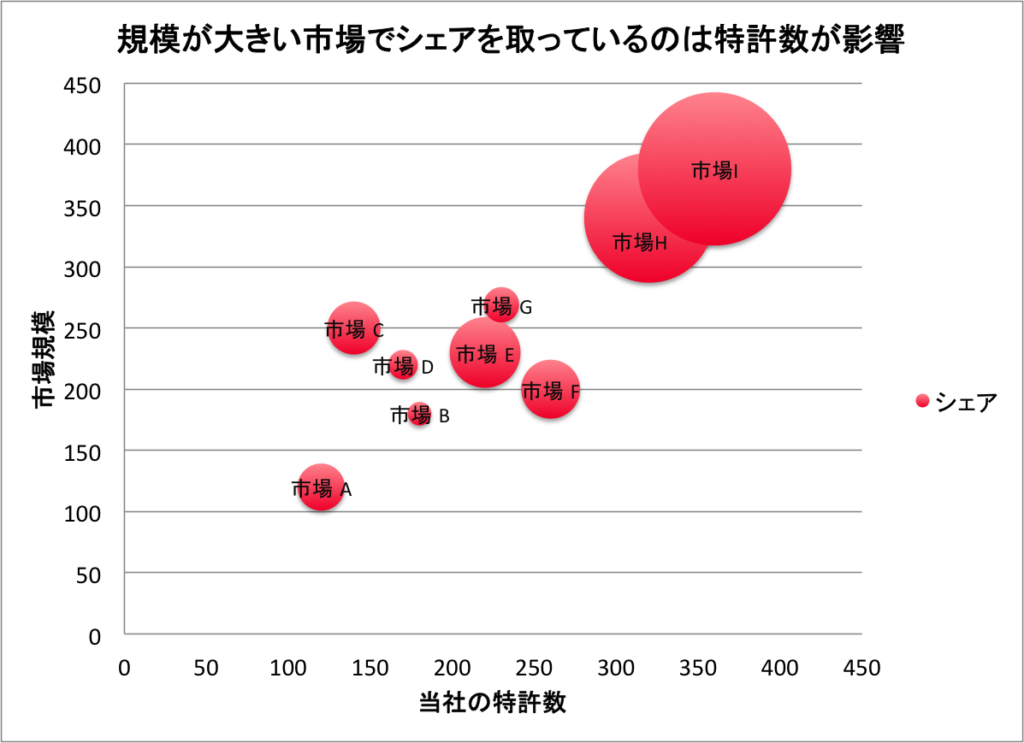
バブルチャート

バブルチャートは、データを視覚的に表現するためのグラフの一種です。

このチャートは、通常の散布図に似ていますが、データポイントを表すために円（バブル）を使用し、3つの要素のデータを表示することができます。

主な特徴は以下の通りです。

軸のデータ:
- バブルチャートには二つの軸（通常はX軸とY軸）があり、これらはそれぞれ異なるデータセットを表します。
バブルのサイズ:
- 各バブルのサイズは、第三のデータ要素を表し、値の大きさに応じてバブルの大きさが変わります。
色やその他の特徴:
- バブルの色やその他の特徴を変えることで、追加のデータカテゴリーやグループを表現することができます。

バブルチャートは、複数の変数を同時に比較し、データの複雑な関係性を理解するのに有効なツールです。

具体例

たとえば、企業の市場シェア（バブルのサイズ）と、その企業の特許数（X軸）および市場規模（Y軸）を同時に示したのが以下の図です。