プロジェクトの工程管理
ここでは、プロジェクトの工程管理を行うために用いられる視覚的なツールについて説明します。
WBS
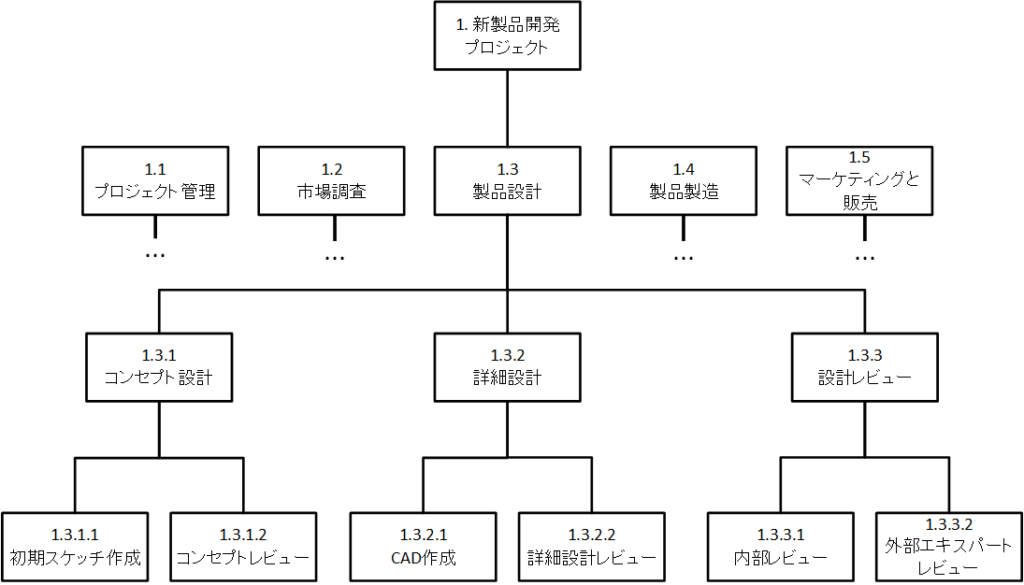
WBS(Work Breakdown Structure)は、プロジェクトを達成するために必要な作業を、より小さな単位に分解し、階層構造で表示する手法です。
具体的には、階層構造の最下位の要素を、コスト見積りとスケジュール作成が行えるレベルにまで分解します。
WBSの作成は、プロジェクトの計画段階において行われる作業の一つで、プロジェクトスコープマネジメントの重要な要素です。その目的は、プロジェクトの成果物とそれを作成するための作業を明確にし、タスクの管理や進捗状況を把握しやすくすることです。
WBSは、プロジェクト全体を俯瞰し、役割分担やリソースの配分を行いやすくすることで、プロジェクトの計画や実行を効率化する役割を果たします。
WBS辞書は、プロジェクト管理において使用されるツールの一つで、WBSで識別・分割された各作業要素の詳細な説明を提供します。WBSはプロジェクトを小さな単位に分割することで、より管理しやすくするための構造です。WBS辞書は、この分割された各要素について、さらに詳細な情報を記載した文書です。
WBS辞書には通常、以下のような情報が含まれます。
- 各作業要素の詳細な説明
- 責任者や担当者
- 必要なリソース(人材、材料、機器など)
- スケジュールや期限
- コスト見積もり
- 品質要件
- 完了基準
- その他関連するリスクや注意点
WBS辞書は、プロジェクトチームが各作業要素に対する明確な理解を持ち、計画通りに進行するための重要な参考資料となります。また、プロジェクトの進行中に発生する可能性のある誤解やコミュニケーションの問題を減少させるのに役立ちます。
ガントチャート
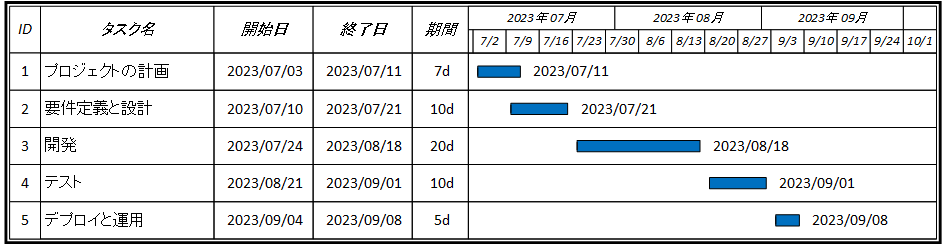
ガントチャートは、プロジェクト管理ツールの一つで、プロジェクトのスケジュールやタスクの進捗状況を視覚的に表現するために使用されます。
横軸に時間の流れを、縦軸にプロジェクトの各タスクや活動を配置し、バーの長さで各タスクの開始日と終了日、期間を示します。
このチャートを用いることで、プロジェクトの全体的なタイムライン、タスク間の関連性や依存関係、重要なマイルストーン、リソースの割り当て状況などを一目で把握することができます。
ガントチャートは、プロジェクトの計画、コーディネーション、コミュニケーションを効果的に支援します。
関連用語
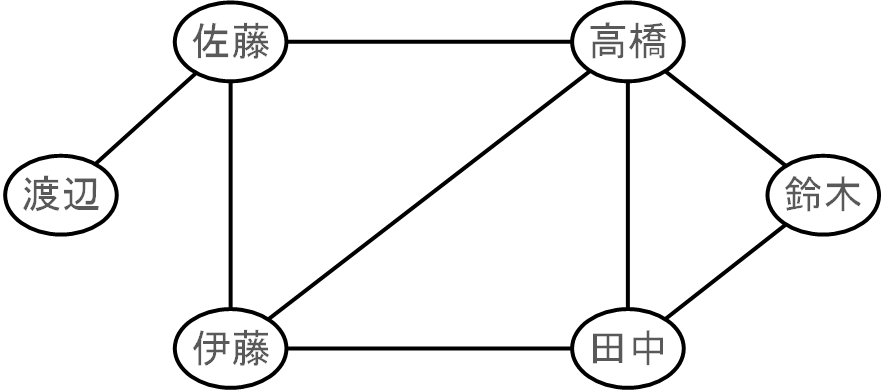
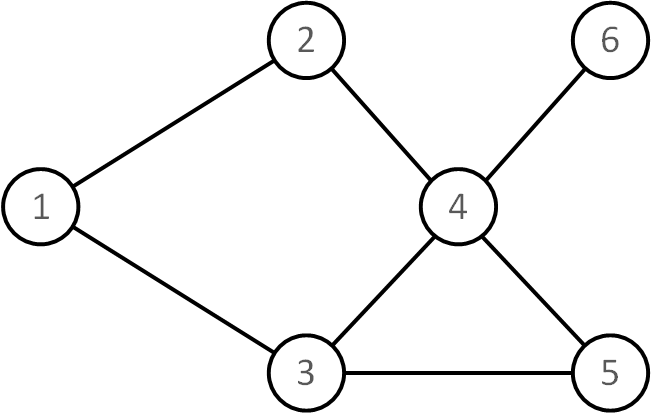
グラフ理論は、数学の一分野であり、ノード(頂点)とそれらを繋ぐエッジ(辺)で構成されるグラフと呼ばれる数学的構造を研究する理論です。(ここでいうグラフとは、一般的な「グラフ」とは別物です)
グラフ理論は、物事の間の関係性やネットワークをモデル化するのに非常に適しています。
基本的な用語には次のようなものがあります。
- 頂点(ノード): グラフの基本要素で、場所や物事を表すことが多いです。
- 辺(エッジ): 2つの頂点を結ぶ線。これにより、頂点間の関係や接続を示します。
- 隣接: 2つの頂点が辺で結ばれている場合、それらの頂点は隣接していると言います。
- 次数: ある頂点に接続されている辺の数を示します。
- 経路: グラフ内の2つ以上の頂点を順番に通る辺の連続のことを指します。経路は、一連の辺を通じて頂点をつなぐ方法や順序を示すものです。
- サイクル: 経路の始点と終点が同じ頂点であるものを指します。
グラフの種類には次のようなものがあります。
- 無向グラフ: 辺に向きがないグラフ。
- 有向グラフ: 辺に始点と終点が存在するグラフ。
- 重み付きグラフ: 辺に「重み」や「コスト」が割り当てられているグラフ。最短経路問題などでよく用いられます。
- 連結グラフ: 任意の2つの頂点間に経路が存在するグラフ。
- 非連結グラフ: いくつかの頂点間に経路が存在しないグラフ。
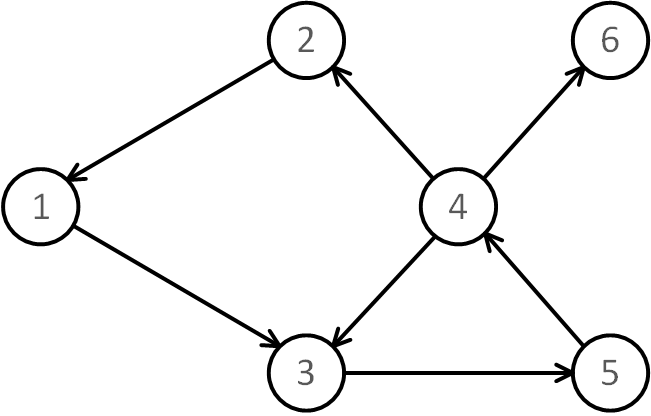
グラフ理論は、コンピュータネットワーク、社会ネットワーク、交通システム、分子構造など、現実世界の多くの問題をモデル化し解析するために利用されます。
その応用例には次節で学習するアローダイアグラムのほか、次のようなものがあります。
- 最短経路問題: 2つの頂点間の最短経路を見つける問題。例えば、Googleマップなど地図上での2つの都市間の最短経路やコンピュータネットワークでの最短通信経路、二つの駅間の最短経路や最小乗り換え回数での経路などの探索。
- 最大流問題: ネットワークの2つの頂点間で、どれだけ多くの「流れ」を送ることができるかを問う問題。例としては、道路やパイプラインの通行能力の最適化が挙げられます。
- 巡回セールスマン問題 (TSP): すべての都市を訪れ、最初の都市に戻る最短のルートを見つける問題。物流や配達の最適化に使用されることが多い。
- 色塗り問題: 頂点や辺に色を塗り、隣接する頂点や辺が同じ色にならないようにする問題。例えば、無線通信での周波数割り当てや時間割の作成など。
- 連結成分の検出: グラフがいくつの独立した部分グラフ(連結成分)に分かれているかを判断する問題。SNSでのコミュニティ検出や、電力ネットワークの独立した部分の検出などに使用される。
- 最小全域木問題: グラフのすべての頂点を最小のコストでつなぐ木を見つける問題。電話回線やネットワークの設計に応用されることが多い。
- ネットワークの堅牢性分析: グラフ上でのノードやエッジの障害に対するネットワークの耐性を評価する。
- 友達の推薦: FacebookのようなSNSプラットフォームで、ユーザーの関連性や類似性を元に新しい友達を推薦する。どのユーザー間に強いつながりやコミュニティが存在するかを特定する。
グラフを用いることで、複雑な関係性や構造をシンプルで理解しやすい形で表現できるため、効率的な問題解決や意思決定を支援する強力なツールとなっています。