目次
代表的なアルゴリズム
探索のアルゴリズム
探索アルゴリズムとは、データの集合から特定の要素を見つけ出すための手順です。これには様々な方法がありますが、ここでは最も一般的な線形探索法と2分探索法について説明します。
線形探索法(Linear Search)
線形探索法は、配列やリストの各要素を順番にチェックして特定の要素を探す最も基本的な探索アルゴリズムです。
動作のプロセス:
- 配列の最初の要素から始めます。
- 各要素を順にチェックし、目的の要素を探します。
- 目的の要素が見つかればその位置を返し、見つからなければ配列の最後まで探索を続けます。
特徴:
- 非常にシンプルで、どのような配列やリストにも適用可能です。
- 配列が大きくなるほど、または目的の要素が配列の後方にあるほど、探索に時間がかかります。
- ソートされていない配列やリストにも適用できます。

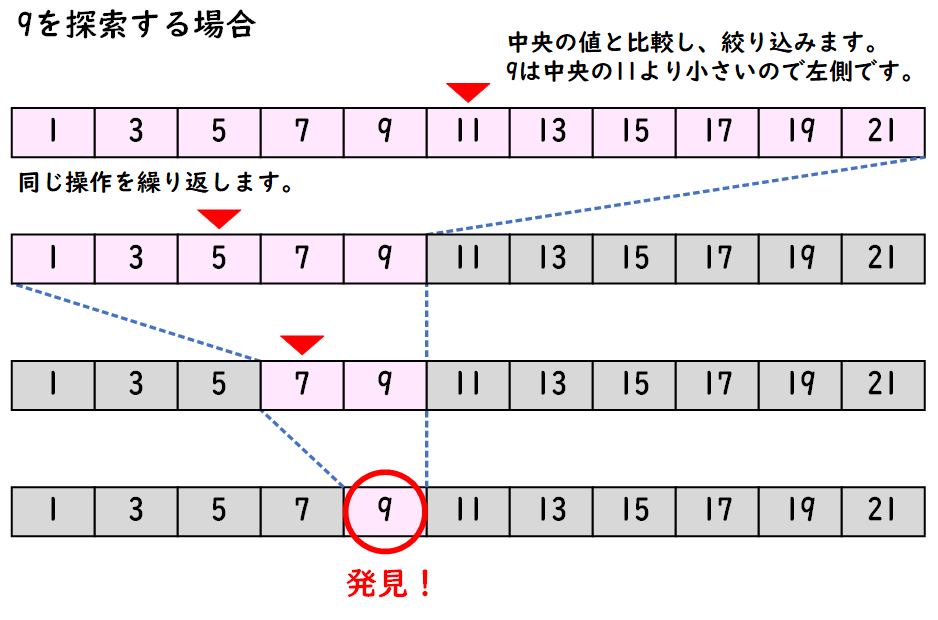
2分探索法(Binary Search)
2分探索法は、ソート済みの配列やリスト内で特定の要素を効率的に探すアルゴリズムです。この方法では、探索範囲を半分に分割していくことで、目的の要素を迅速に見つけます。
動作のプロセス:
- 配列の中央の要素を調べます。
- 目的の要素が中央の要素より大きい場合、探索範囲を中央の要素より右側に絞ります。
- 目的の要素が中央の要素より小さい場合、探索範囲を中央の要素より左側に絞ります。
- このプロセスを繰り返し、目的の要素を見つけるか、探索範囲がなくなるまで続けます。
特徴:
- 非常に効率的で、大きなデータセットでも高速に動作します。
- 探索する配列やリストは事前にソートされている必要があります。
線形探索法と2分探索法の比較
線形探索法と2分探索法を比較した際の主な特徴、特に効率面について詳しく説明します。
線形探索法
- 効率: 効率は比較的低いです。最悪の場合(目的の要素が配列の最後にあるか、存在しない場合)、配列のすべての要素をチェックする必要があります。つまり、n個の要素がある場合、最大n回の比較が必要です。
- 計算量: 平均計算量と最悪計算量は共に O(n) です(nは要素数)。
- 特徴: 配列やリストがソートされていなくても使用できます。単純で理解しやすいですが、データ量が多いほど非効率的になります。
2分探索法
- 効率: 非常に高い効率を持ちます。探索範囲を各ステップで半分に減らすため、必要な比較回数は大幅に減少します。
- 計算量: 最悪計算量と平均計算量は共に O(log n) です。これは、配列のサイズが倍になっても、追加のステップは1つだけで済むことを意味します。
- 特徴: 事前に配列がソートされている必要があります。大量のデータに対して非常に効率的ですが、ソートされていないデータには適用できません。
比較
- データ量: 小さいデータセットでは、線形探索法の単純さが有利になることがありますが、データ量が多くなると2分探索法の効率の良さが顕著になります。
- データの整理: 線形探索法はソートされていないデータに使用できますが、2分探索法はソートされたデータにのみ適用可能です。
- 実用性: 実際のアプリケーションでは、データの量やソートの有無に基づいて、これらの探索方法を選択する必要があります。
総じて、2分探索法はデータが多くソートされている場合に非常に効率的ですが、データが少ないかソートされていない場合は線形探索法の方が適している場合があります。
