システムの信頼性
システムの信頼性を高めるためには、定期的なメンテナンスとシステムのアップデート、バックアップ・冗長化、監視・運用管理、セキュリティ対策などが必要であり、これらの要素が組み合わさった総合的な対策が求められます。
それではシステムの信頼性を定量的に捉えるにはどうしたらよいでしょうか?
以下のような、稼働と故障を繰り返すシステムを例にとって考えてみましょう。

システムの信頼性を定量的に捉えるための指標には、次のようなものがあります。
平均故障間隔
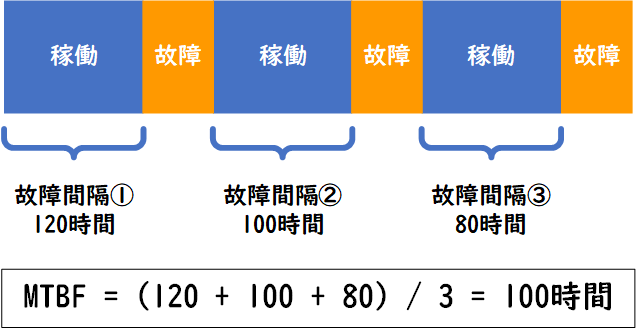
平均故障間隔(MTBF:Mean Time Between Failures)は、故障から次の故障までの平均時間、つまりシステムが正常に稼働している平均時間を表す指標で、長いほど信頼性が高いことを示します。図の青色部分の平均のことです。
\( \displaystyle {}\text{MTBF} = \frac{\textbf{各故障間隔の合計}}{\textbf{故障回数}} \)
平均修復時間
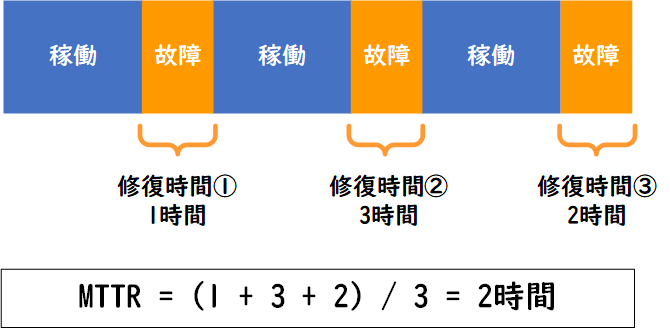
平均修復時間(MTTR:Mean Time To Repair)は、故障発生から復旧までの平均時間を表す指標で、短いほど信頼性が高いことを示します。図の黄色部分の平均のことです。
\( \displaystyle {}\text{MTTR} = \frac{\textbf{各修復時間の合計}}{\textbf{故障回数}} \)
稼働率
稼働率はシステムが正常に稼働している時間の割合を表す指標で、高いほど信頼性が高いことを示します。可用性が99%以上であることが求められる場合もあります。
\( \displaystyle {}\textbf{稼働率} = \frac{\textbf{平均故障間隔}}{\textbf{平均故障間隔}+\textbf{平均修復時間}} = \frac{\text{MTBF}}{\text{MTBF}+\text{MTTR}} \)
直列システムと並列システムの稼働率
直列システムの稼働率
直列システムの稼働率は、以下のように計算されます。
\( R = R_1 \times R_2 \times R_3 \times \ldots \times R_n \)
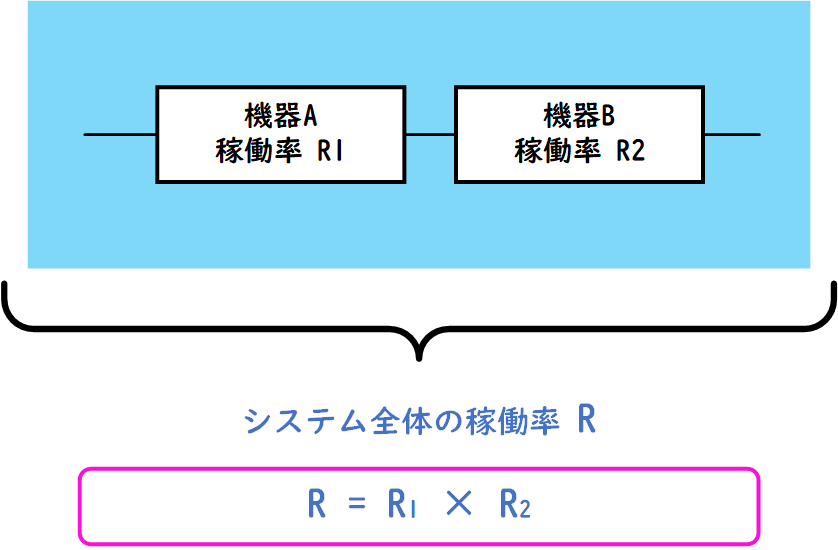
ここで、Rはシステム全体の稼働率、R1〜Rnは各機器の稼働率を表します。
直列システムでは、複数の機器がつながっているため、どれか1つでも故障した場合には、全体の稼働率が下がってしまいます。そのため、各機器の稼働率が高いほど、システム全体の稼働率も高くなります。
例えば、3つの機器が直列につながっていて、それぞれの稼働率が90%、95%、98%だった場合、全体の稼働率は、
\( \displaystyle {}0.9 \times 0.95 \times 0.98 = 0.8346 \quad {\text{(83.46%)}}\)
となります。
並列システムの稼働率
並列システムの稼働率は、以下のように計算されます。
\( R = 1 – (1 – R_1) \times (1 – R_2) \times (1 – R_3) \times \ldots \times (1 – R_n)\)
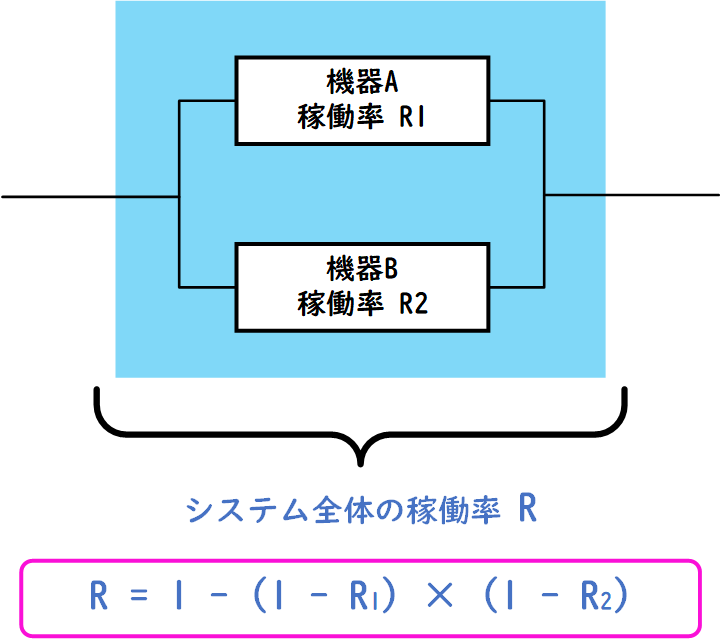
ここで、Rはシステム全体の稼働率、R1〜Rnは各機器の稼働率を表します。
並列システムでは、複数の機器が並列につながっているため、各機器が独立して動作し、どれか1つが故障しても他の機器は動作を継続することができます。そのため、各機器の稼働率が高いほど、システム全体の稼働率も高くなります。
例えば、3つの機器が並列につながっていて、それぞれの稼働率が90%、95%、98%だった場合、全体の稼働率は、
\( 1 – (1 – 0.9) \times (1 – 0.95) \times (1 – 0.98) = 0.9989 \quad {\text{(99.89%)}}\)
となります。
並列システムの稼働率は、故障する確率の余事象として計算されます。余事象とは、事象Aに対して、Aが起こらないという事象のことで、余事象の確率について、以下の関係が成り立ちます。
Aが起こらない確率 = 1−Aが起こる確率
これを並列システムの稼働率に当てはめて考えると、
並列システムが故障しない確率 = 1−並列システムが故障する確率
つまり、以下のように言い換えることができます。
並列システムの稼働率 = 1−(すべての部品が故障する確率)
たとえば、二つの部品からなる並列システムで、各部品がそれぞれ故障する確率が(1-R1)と(1-R2)だとすると、
稼働率 = 1−(1-R1)×(1-R2)
このように、並列システムの稼働率は、すべての部品が同時に故障する確率の余事象として計算されます。
直列システムと並列システムの稼働率を例え話で説明します。
想像してみてください、あなたと友人が公園でピクニックをする約束をしたとします。
直列システムの稼働率:
公園に行くためには三つの連続した橋を渡る必要があります。これは直列システムに相当します。最初の橋を渡り、次に二番目の橋、そして最後に三番目の橋を渡る必要があります。
もし、最初の橋が壊れていたら、二番目と三番目の橋が無事であっても、公園にたどり着けません。同様に、最初と二番目の橋が無事でも、三番目の橋が壊れていたら公園に行けません。つまり、三つの橋のうち一つでも壊れていると、公園にたどり着くことができないのです。直列システムでは、一つでも故障すると全体が機能しなくなるので、稼働率は低くなります。
並列システムの稼働率:
次に、公園に行くための三つの橋がそれぞれ独立して存在し、どの橋を渡っても公園にたどり着けるケースを考えます。これは並列システムに相当します。
仮に、一つの橋が壊れていても、残りの二つの橋が無事であれば公園に行くことができます。二つの橋が壊れていたとしても、最後の一つの橋が無事ならやはり公園に行けます。つまり、全ての橋が同時に壊れない限り、公園にたどり着けるのです。並列システムでは、一部が故障しても他の経路が動作するため、稼働率は高くなります。
まとめ:
直列システムでは、全ての橋が連続して機能しなければならず、一つでも壊れると公園にたどり着けません。一方、並列システムでは、複数の独立した橋があり、一部が壊れても他の橋を使って公園にたどり着けるため、稼働率が高くなります。このように、直列システムは一つの故障で全体が停止するのに対し、並列システムは一部の故障に対しても柔軟に対応できるという特徴があります。
