業務分析手法
業務分析手法とは、業務プロセスやシステムを分析し、業務の効率化や品質向上、問題解決などを目的とした手法のことです。
代表的な手法としては以下のようなものがあります。
特性要因図
特性要因図は、問題の原因を分析するためのツールで、魚の骨の形をした図を用いて視覚的に表現します。
問題が発生した場合、この図を使用して、原因をさまざまなカテゴリに分け、それぞれの要因を明確にしていきます。
一般的には、人・方法・材料・機械・測定・環境といったカテゴリが用いられます。特性要因図を使うことで、問題の根本原因を特定し、対策を立てることが容易になります。
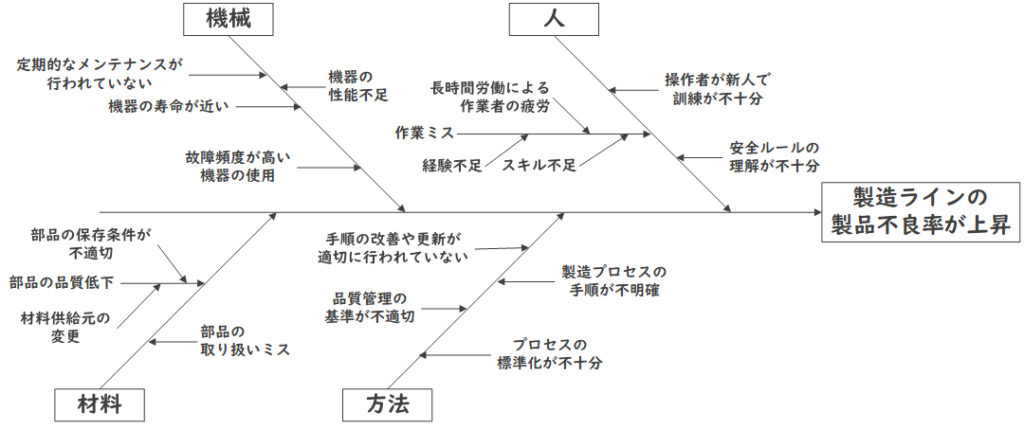
特性要因図は、1956年に日本人の石川馨によって考案されたため「石川ダイアグラム(Ishikawa Diagram)」とも呼ばれます。また、その形状が魚の骨に似ていることから「魚の骨図(フィッシュボーン図:Fishbone Diagram)」とも呼ばれています。
パレート図
パレート図とは、分類項目ごとのデータを大きい順(降順)に並べた棒グラフと、その累積の構成比を表す折れ線グラフを組み合わせたグラフです。
どの項目が全体に対してどの程度の影響を持っているかを直感的に理解するのに適したグラフで、製品管理や顧客層分析などで役立ちます。
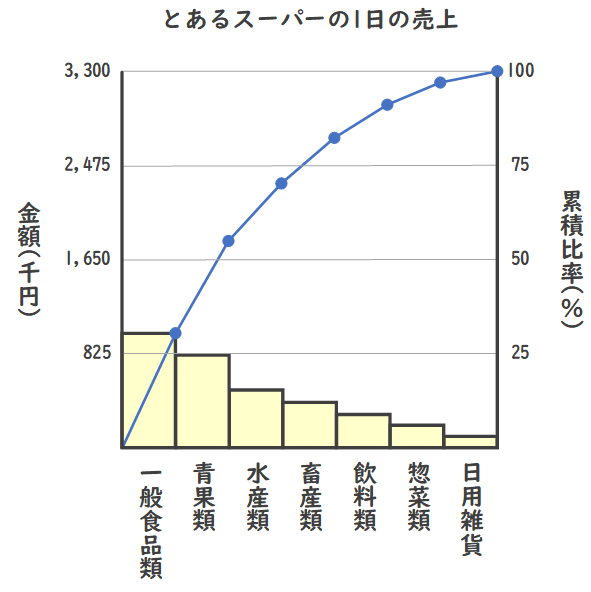
パレート図は、原因と結果の関係を視覚化するためによく使われる統計的なツールです。
この図は、イタリアの経済学者ヴィルフレド・パレートにちなんで名付けられました。パレートが発見した原理、すなわち「パレートの法則」または「80:20の法則」としても知られているものを基にしています。
この法則は、結果の大部分(約80%)は原因の少数(約20%)によってもたらされるという考え方を示しています。
ABC分析
パレート図を利用した分析手法にABC分析があります。
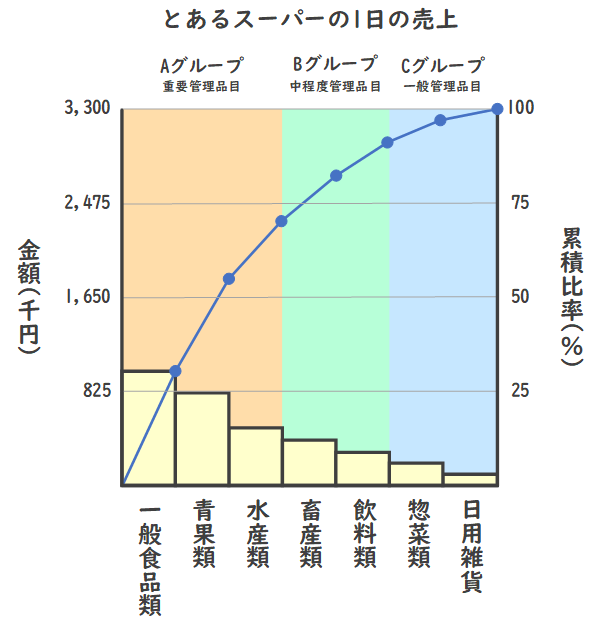
ABC分析は、在庫管理、顧客管理、売上分析など様々な分野で使用される手法で、項目を重要度に基づいて3つのグループ(A、B、C)に分類します。
この分析は、資源を最も効果的に割り当てるために重要な項目に焦点を当てることを目的としています。
- Aグループ: 最も重要な項目で、全体の成果に大きく貢献する少数の要素(例えば、売上の80%を生み出す20%の顧客や製品)。
- Bグループ: 中間的な重要度の項目で、Aに次ぐ貢献度を持ちます。
- Cグループ: 最も重要度が低い項目で、数は多いが全体に対する貢献度は小さい要素(例えば、売上の5%しか生み出さない50%の顧客や製品)。
ABC分析により、経営資源の最適な配分が可能となり、効率的な意思決定や優先順位付けを支援します。
ヒストグラム
ヒストグラムは、データの分布を表すグラフで、数値データを一定の間隔(階級)に分割し、各階級の度数(出現回数)を縦軸にとった棒グラフで表示します。
これにより、データの全体像や偏りを把握できます。
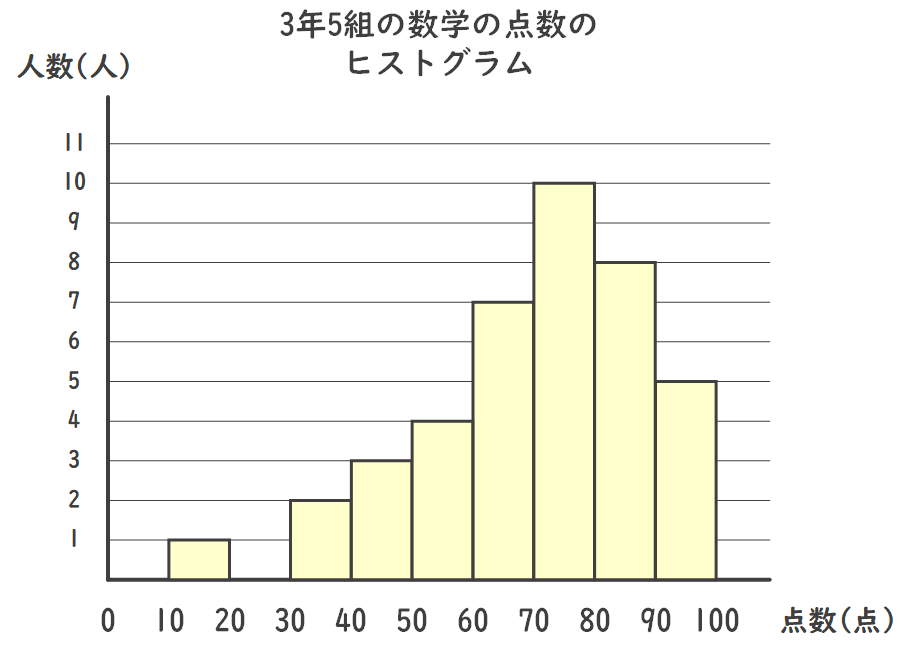
| 階級(点数) | 度数(人) |
|---|---|
| 90 ~ 100 | 5 |
| 80 ~ 89 | 8 |
| 70 ~ 79 | 10 |
| 60 ~ 69 | 7 |
| 50 ~ 59 | 4 |
| 40 ~ 49 | 3 |
| 30 ~ 39 | 2 |
| 20 ~ 29 | 0 |
| 10 ~ 19 | 1 |
| 0 ~ 9 | 0 |
| 合計 | 40 |
ヒストグラムと棒グラフは、見た目が似ているため混同されやすいですが、実際には異なるデータを表現するためのグラフです。
- ヒストグラム:
- 連続的なデータを表現するときに使われます。
- データの分布や頻度を示すため、隣接する棒の間には空間がありません。
- 例: 年齢別の人数や試験の点数別の生徒数など。
- 棒グラフ:
- カテゴリデータを表現するときに使われます。
- 各カテゴリの値を比較するため、棒の間には間隔があります。
- 例: 商品カテゴリごとの売上や都市別の人口など。
箱ひげ図
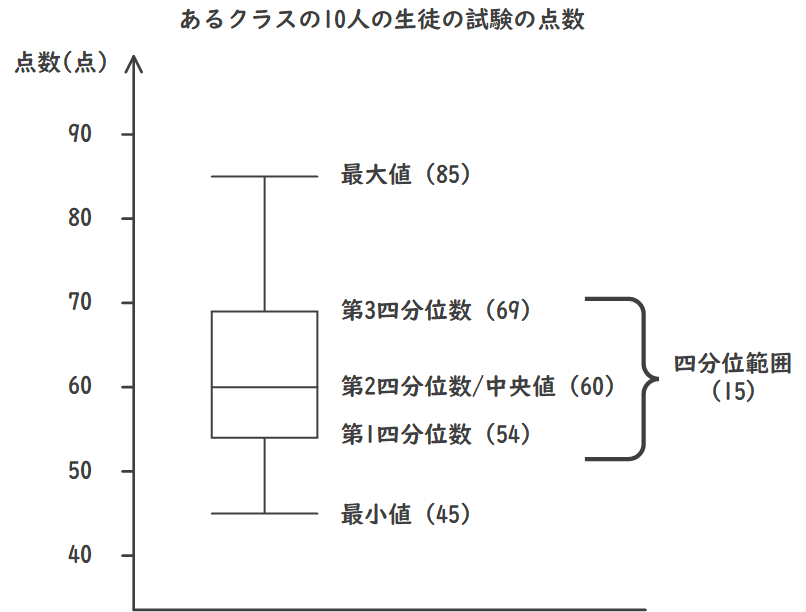
箱ひげ図は、データの分布やばらつきを視覚的に表すグラフで、データの最小値、第1四分位数、中央値(第2四分位数)、第3四分位数、最大値といった統計量を箱とひげで表現します。
これにより、データの中心傾向やばらつき、外れ値を一目で確認できます。
例として、あるクラスの10人の生徒の試験の点数を考えます。
データセット: 45, 52, 54, 55, 59, 61, 68, 69, 72, 85
- 最小値(Minimum): 最小の点数を示します。
- 最小値 = 45
- 第1四分位数(Q1): データを小さい順に並べたとき、下から25%の位置にあたる点数。
- Q1=54
- 中央値(Median, Q2): データを小さい順に並べたとき、中央にある点数。データの数が偶数の場合は、中央の2つのデータの平均を取ります。
- 中央値 = (59+61)/2=60
- 第3四分位数(Q3): データを小さい順に並べたとき、下から75%の位置にあたる点数。
- Q3=69
- 最大値(Maximum): 最大の点数を示します。
- 最大値 = 85
- IQR(四分位範囲): Q3−Q1
- IQR=69−54=15
箱ひげ図における最小値、第1四分位数、中央値(第2四分位数)、第3四分位数、最大値をたとえ話で説明します。
ここではロールケーキを4等分にカットするケースを考えてみましょう。最初にロールケーキの左端を最小値、右端を最大値とみたてます。
ここから4等分するためにはナイフを3回入れる必要があります。最初にロールケーキの真ん中にナイフを入れます。この切り口が中央値(第2四分位数)に相当します。
次に、このカットでできた半分ずつのロールケーキをさらにそれぞれの真ん中でカットします。こうすることで、4等分にできます。これによって出来上がった二つの新しい切り口のうち、左側が第1四分位数、右側が第3四分位数となります。
※ただし、実際の箱ひげ図におけるデータのばらつきとロールケーキの形状は一致しないこともあるため、この例えはあくまで四分位数の概念を理解するためのものとしてください。
管理図
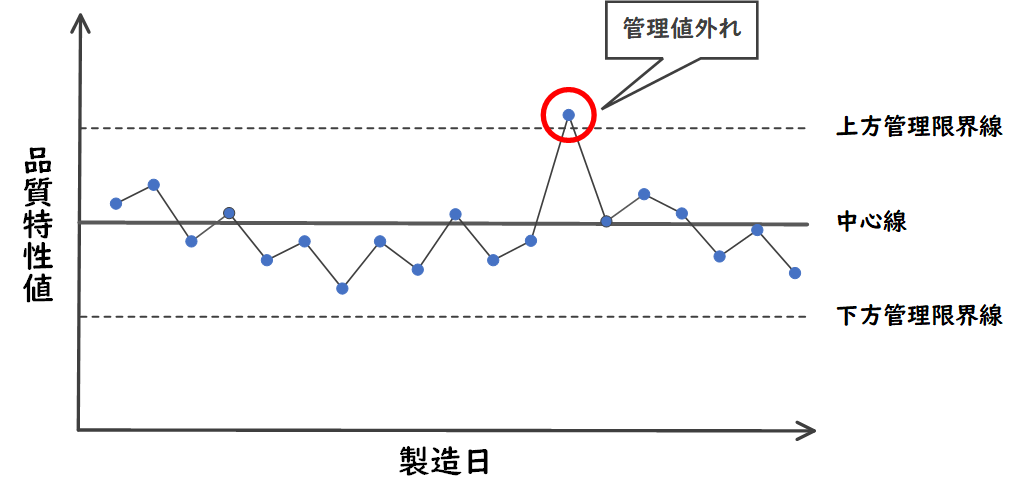
管理図は、プロセスの安定性や品質を監視するためのグラフで、プロセスから得られるデータを時系列にプロットし、中心線(平均値)と管理限界線(上限と下限)を表示します。
データが管理限界線内にある場合、プロセスは安定しているとみなされますが、管理限界線線を超えると、プロセスに異常があると判断されます。
これにより、プロセスの問題を特定し、改善に取り組むことができます。
ヒートマップ
ヒートマップとは、データの密度や強度を色の濃淡や温度で視覚的に表現するグラフィカルな表示方法のことを指します。色の濃淡や色の違いによって、データの高低や差を瞬時に捉えることができます。
具体的な使用例としては、以下のようなものがあります。
- Webサイトの利用状況:ウェブページ上でのユーザーのクリックやマウスの動きを色で示し、どの部分がよく見られているか、どの部分にユーザーの関心が集まっているかを分析します。
- 地理的なデータの分析:ある地域や場所に関する情報を地図上で色の濃淡で表現し、活動の多い場所や問題のある場所を特定します。
- データセットの特徴:大量のデータや統計を一覧表示する際に、特定の値や頻度の高さを色で表現し、全体の傾向や特徴をすぐに把握するのに役立てます。
ヒートマップは視覚的に直感的であり、多量の情報を一目で理解するのに非常に効果的です。しかし、正確な数値や細かい情報が必要な場合には、他の詳細な分析手法と組み合わせることが推奨されます。
レーダーチャート
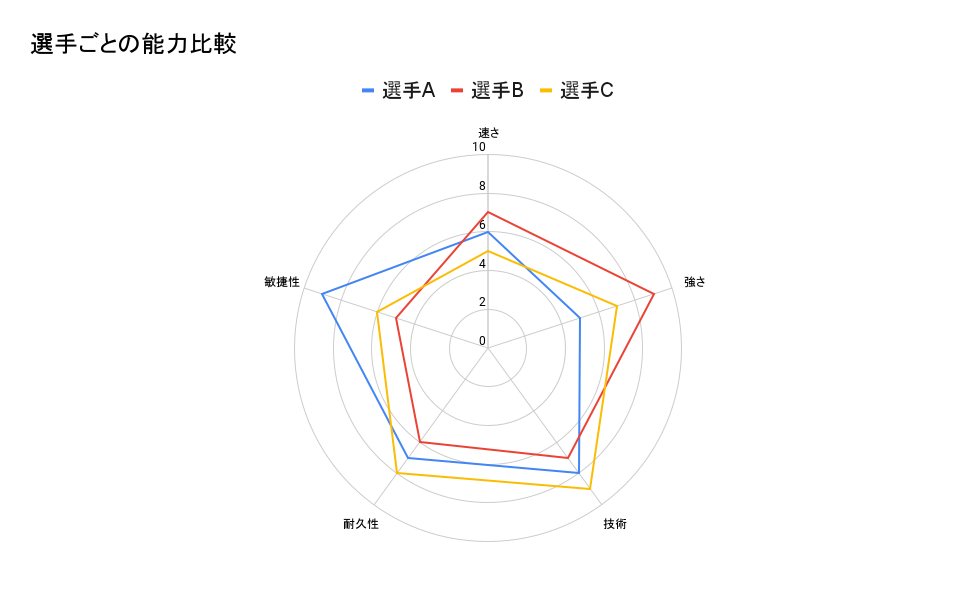
レーダーチャート(またはスパイダーチャート、ウェブチャートとも呼ばれます)は、多次元のデータを視覚的に表珆するのに適したグラフです。
このチャートは、中心から外側に向かって伸びる複数の軸(通常は放射状)を持ち、各軸が一つの変数を表します。データポイントは軸に沿ってプロットされ、線または曲線で連結されて一つの形を形成します。これにより、複数の変数を含む項目やグループを直接比較することが可能になります。
レーダーチャートは、特に異なる項目のパフォーマンスを多面的に比較する場合(例えば、商品の複数の品質属性の評価、人材のスキルセット評価など)に有効です。
また、複数の項目が同時に比較される場合には、それぞれの形状を重ねて表示することで、直感的な視覚比較を行うことができます。
データの視覚化
ロジックツリー
ロジックツリーは、複雑な問題を解決するために、その問題を小さな部分に分解し、各部分の関連性や因果関係を明確にする図式です。
このツリーは、根(問題の出発点)から始まり、枝(可能な要因や選択肢)を通じて葉(結論や解決策)に至るまでのプロセスを図示します。
この手法は、戦略立案、意思決定のプロセス、原因分析など、多岐にわたる分野で活用されています。
たとえば、ある企業が「利益を増やしたい」という目標を持っているとします。この大きな目標をロジックツリーに落とし込むと、以下のようになります。
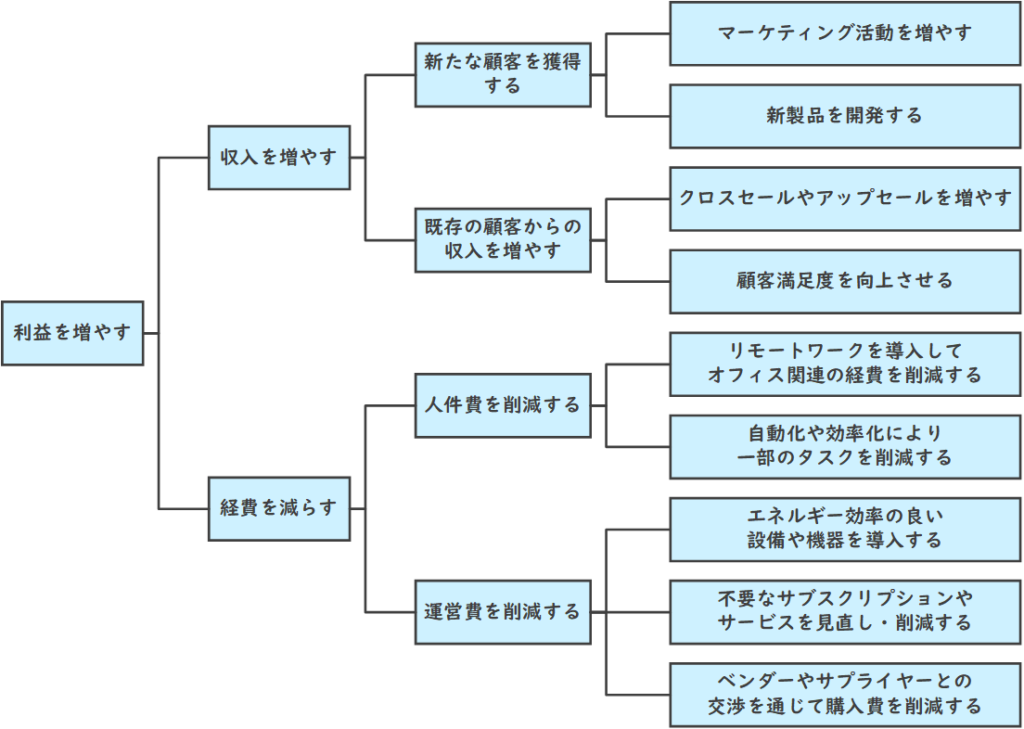
このようにロジックツリーを使用することで、大きな問題や目標を具体的な行動に落とし込むことができ、それぞれが全体の目標にどのように貢献するのかを明確にすることができます。
マトリックス図
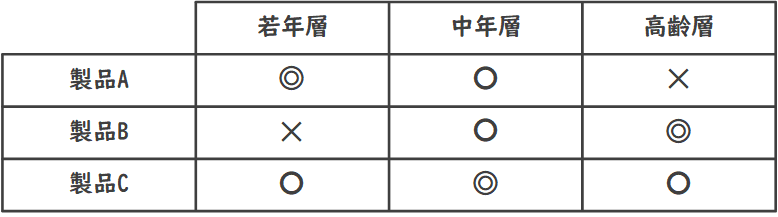
マトリックス図は、二つの異なる属性間の関係性を表現する図です。
表の形をしており、行と列にそれぞれ異なる属性を配置し、交差するセルに関係性の強さや評価を記入します。
例えば、製品と顧客の関係や、プロジェクトの要素間の相互依存関係などを表現する際に利用されます。
モザイク図
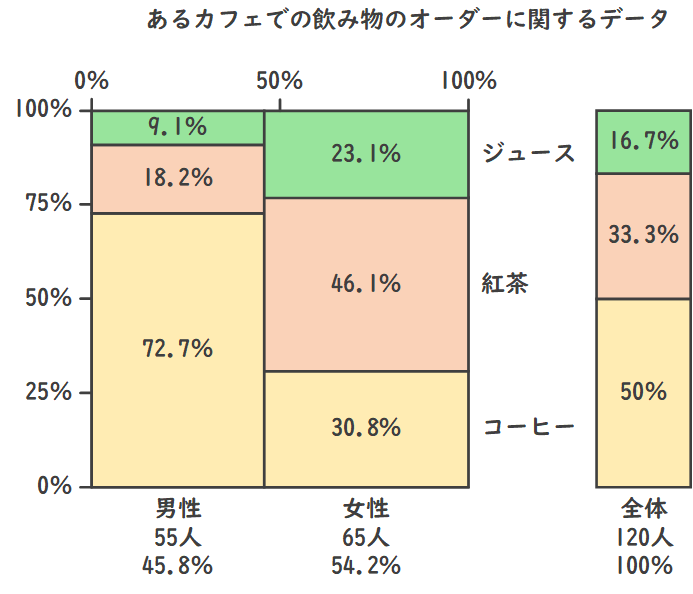
モザイク図は、カテゴリー別のデータを色や形の異なるブロックで表現し、全体のパターンや傾向を視覚的に表す図です。
具体的には、2つのカテゴリ変数を縦軸・横軸に取り、各カテゴリの組み合わせの度数(頻度)をそれに比例する面積の長方形で表現します。
主に統計データの分析や比較に用いられ、異なるグループ間での比率や差異を一目で把握することができます。
コンセプトマップ
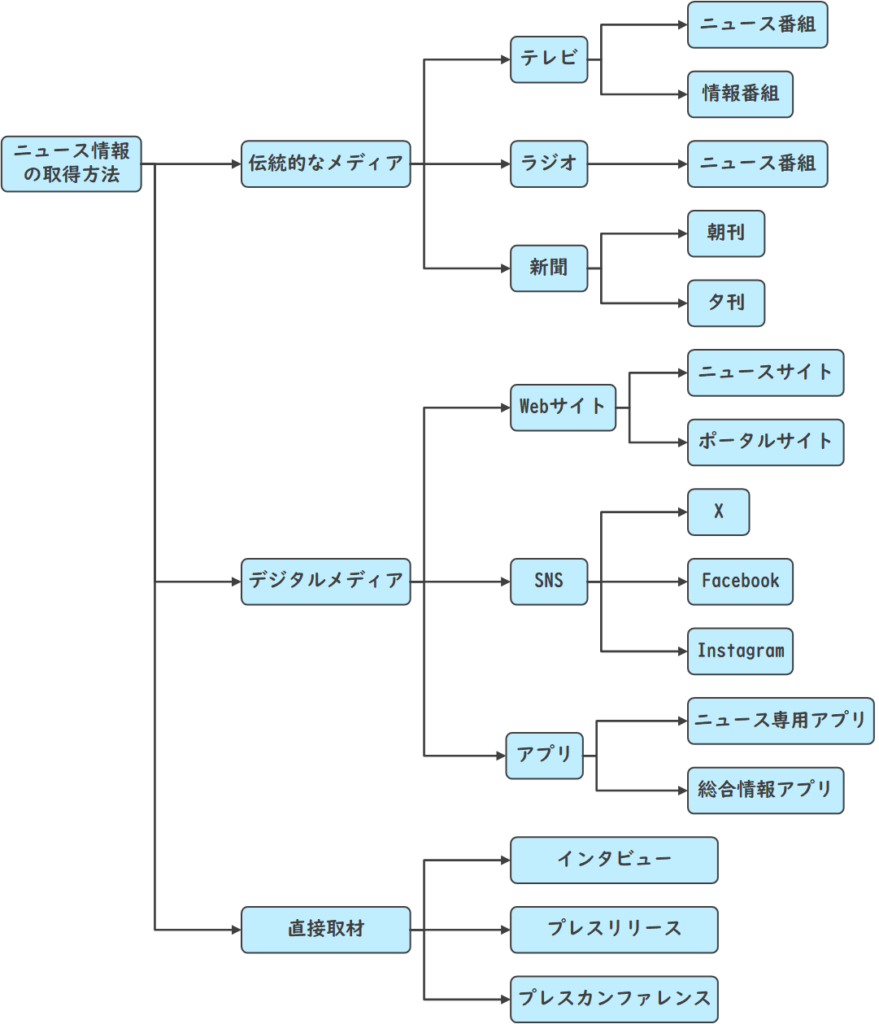
コンセプトマップは、概念やアイデア間の関係を視覚化するための図です。
コンセプトマップは、概念を表すノード(円や四角形などの形で表現)と、ノード間の関係を示す線や矢印で構成されます。関係の性質や方向性を表すラベルが線や矢印に付けられることもあります。
以下は、人々のニュース情報の取得方法に関するコンセプトマップです。