減価償却
減価償却とは、会社が長期的に使用するために購入した資産(例:機械、建物、コンピュータなど)が、時間の経過と共にその価値を失っていくことを会計上で表現する方法のことを指します。
これは、資産の購入にかかった金額(取得価額)から、その資産がもはや役に立たなくなった時点での価値(残存価値)を引いたものを、資産の使用可能な寿命(通常は年数)で割り、一定期間ごと(通常は年次)に資産の価値を減らし、経費として計上していくことを意味します。
例えば、ある会社が12万円でコンピュータを購入し、その使用可能な寿命を4年と見積もったとします。この場合、後述する定額法で見積もれば、コンピュータの価値は、毎年(12万円 / 4年 =)3万円ずつ減少することになります。これが減価償却の基本的な考え方です。
減価償却は、会社の財務状況を正確に把握するために必要です。
資産を一括で経費として計上すると、購入した年度の利益が大幅に下がり、次の年度以降の利益が過大に見える可能性があります。
しかし、減価償却を行うことで、資産のコストをその使用期間に均等に分散させることができ、より現実的な利益を計上することが可能になります。
この減価償却にはいくつかの方法がありますが、主なものとして「定額法」と「定率法」があります。
定額法
これは非常に直感的な方法で、資産の取得価額を後述する法定耐用年数で割り、毎年一定の金額を減価償却費として計上します。
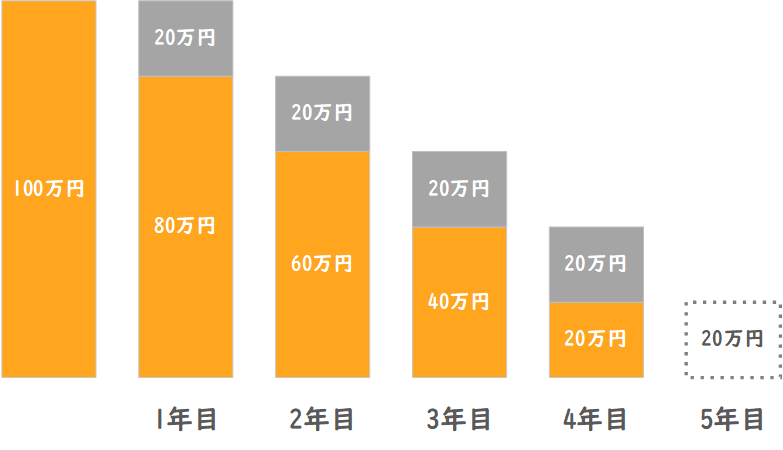
例えば、取得価額が100万円で法定耐用年数が5年の場合、毎年20万円を減価償却費として計上することになります。これにより、資産の価値が均等に時間とともに減少することを表現します。
定額法は、主に無形固定資産(例えばソフトウェアなど)に適用されます。
定率法
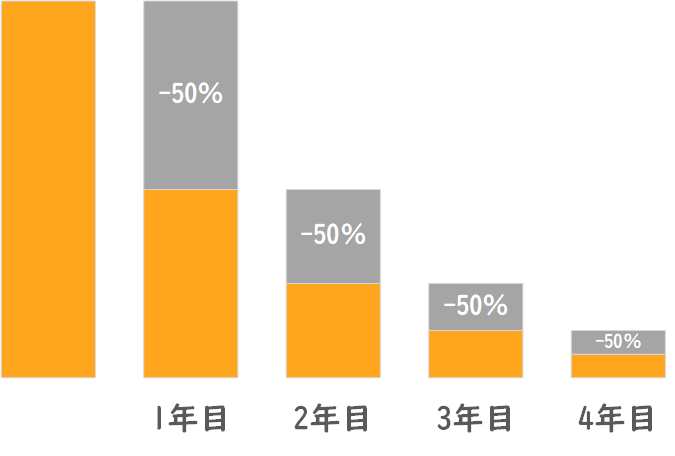
定率法は、資産の価値が時間とともに急速に減少すると考えられる場合に用いられます。
毎年の減価償却費は前年末の帳簿価額(取得価額からこれまでの減価償却額を引いたもの)に一定の率(定率)を掛けて求めます。この方法では初年度の減価償却額が大きく、年々その額は減少していきます。これは、資産の価値が初期に大きく減少し、その後は減少率が緩やかになるという概念を反映しています。
定率法は、主に有形固定資産(例えば機械や設備など)に適用されます。
法定耐用年数
また、資産の使用可能な年数を耐用年数といい、資産の種別ごとに国が法定耐用年数として定めています。これには以下のような意義があります。
- 減価償却費の正確な計算: 法定耐用年数により、資産の価値減少を時間に応じて適切に計算し、決算書に反映させることができます。これにより、企業の財務状況を正確に把握することが可能となります。
- 納税者間の公平性の保証: 資産の使用可能な期間を納税者が自由に決定できると、課税における公平性が損なわれる可能性があります。しかし、法定耐用年数を設定することで、全ての納税者に対する公平性を保つことができます。
- 納税者の負担軽減: 資産の耐用年数を個々の納税者が自分で決定すると、それによる計算の手間や負担が増えます。法定耐用年数を設けることで、納税者のこのような負担を軽減することができます。
具体的な資産の法定耐用年数の例としては、パソコンは4年、サーバーは5年、ソフトウェアは目的により3年(販売用の原本、研究開発目的)または5年(その他)となっています。
減価償却を理解するために、農家が新しいトラクターを購入したというシチュエーションを考えてみましょう。
この農家は100万円で新しいトラクターを購入し、その寿命を10年と見積もりました。このトラクターを使って作物を育て、収穫を行うことで収入を得ます。しかし、トラクターは購入した瞬間から使用による劣化や経年劣化が始まり、価値が徐々に下がっていきます。それを考慮しないと、会計上の問題が生じます。
例えば、農家がトラクターのコスト全額を購入年度の経費として計上すると、その年の利益はトラクターの価格分だけ大幅に減少します。次の年度以降、トラクターのコストを計上しないため、利益が実際よりも大きく見える可能性があります。
そこで減価償却が登場します。減価償却の定額法を用いた場合、トラクターのコストを10年間で均等に分けて計上します。つまり、毎年10万円ずつ経費として計上することになります。
このようにして、トラクターのコストをその利用期間にわたって分散させることで、各年度の収益をより現実的に反映することができます。これが、減価償却の本質的な考え方となります。
期待値
期待値とは、事象の発生確率とその事象が発生した際の結果の値を掛け合わせたものを全ての可能な事象に対して加算したものです。
つまり、期待値は確率的な視点から見た「平均の値」であり、その事象が何度も繰り返されるときの平均的な結果を示します。
期待値の例
具体的な例を挙げて説明しましょう。
あなたがサイコロを振るゲームに参加して、1が出たら100円、2が出たら200円、…、6が出たら600円を貰えるとします。
| 1 | 2 | 3 | 4 | 5 | 6 |
| 100円 | 200円 | 300円 | 400円 | 500円 | 600円 |
このとき、それぞれの数字が出る確率は1/6です。そして、それぞれの数字が出たときの利益はその数字そのもの(100円, 200円, …, 600円)です。したがって、このゲームの期待値は次のように計算できます。
\( \displaystyle {}(\frac{1}{6}\times100\textbf{円})+(\frac{1}{6}\times200\textbf{円})+(\frac{1}{6}\times300\textbf{円})+(\frac{1}{6}\times400\textbf{円})+(\frac{1}{6}\times500\textbf{円})+(\frac{1}{6}\times600\textbf{円}) = 350\textbf{円}\)
つまり、このゲームを何度もプレイすると、平均的に一回あたり350円を貰えるということを期待値は示しています。
期待値は、様々な事象の平均的な結果や予測を求める際に利用されます。以下に具体例を挙げて説明します。
- 事業の投資判断:
- 新製品を市場に投入する際、成功した場合の利益が500万円、失敗した場合の損失が300万円で、成功する確率が60%だとすると、
- 期待値 = 0.6 × 500万円 – 0.4 × 300万円 = 180万円
- この場合、投資が平均的に180万円の利益を生むと期待できます。
- 保険業:
- 保険会社が新しい保険商品を提供する場面を考えます。年間1万円の保険料で、事故が起きた場合に300万円を支払うとします。事故が起こる確率が0.5%だとすると、
- 期待値 = 0.005 × (1 – 300万円) + 0.995 × 1万円 = -0.5万円
- この保険商品を提供すると、会社は長期的に1件あたり平均で5000円の損失が発生すると予測されます。
- 農業:
- 農家が新しい種の作物を植える場面を考えます。普通の種より収穫量が20%増加する可能性が70%、収穫が普通の種と同量になる可能性が30%だとします。通常の収穫量での利益が10万円だとすると、
- 期待値 = 0.7 × (10万円 × 1.2) + 0.3 × 10万円 = 114,000円
- 新しい種を植えることで平均的に14,000円の利益増を期待できることがわかります。
- 製薬業界:
- 新しい薬の開発に投資する場面を考えます。成功すれば10億円の利益が見込めますが、失敗すると3億円の損失が生じるとします。成功確率が10%とすると、
- 期待値 = 0.1 × 10億円 – 0.9 × 3億円 = -1.7億円
- この新薬の開発プロジェクトは、平均的に1.7億円の損失が予測されることがわかります。
- 宝くじの購入:
- 1000円の宝くじがあり、1%の確率で100万円当たるとします。
- 期待値 = 0.01 × (100万円 – 0.1万円)- 0.99 × 0.1万円 = 0.9万円
- この期待値は1枚の宝くじにつき平均9,000円の価値があることを示します。ただし、実際には1000円しか支払っていないので、何度も宝くじが発売されれば利益を得る可能性があるとも解釈できますが、大多数の場合は当たらないため、購入者が損をする可能性が高いとも言えます。
このように、期待値は不確実性が高いシチュエーションでの意思決定をサポートするための有用なツールとなります。リスクを考慮しつつ、最も効果的な選択をするための指標として使用されます。
