論理演算
論理演算は、真(True)と偽(False)の2通りの値の間で行われる演算であり、真を1、偽を0に対応付けた2進数で表すことができます。ただし、通常の加算とは異なり、桁上がりを考慮しないのが特徴です。
論理演算には論理和(OR)、論理積(AND)、否定(NOT)、排他的論理和(XOR)などがあります。
真理値表
論理演算の結果を表す真理値表は、入力された真偽値に対して演算結果がどのようになるかを示しています。
例えば、「A AND B」の真理値表では、AとBが両方とも真である場合のみ、結果が真となります。
| A (入力) | B (入力) | A AND B (出力) |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
ベン図
また、論理演算を理解する際には、ベン図を使うと分かりやすくなります。ベン図は集合を図で表現する方法で、論理演算の結果を視覚的に示すことができます。
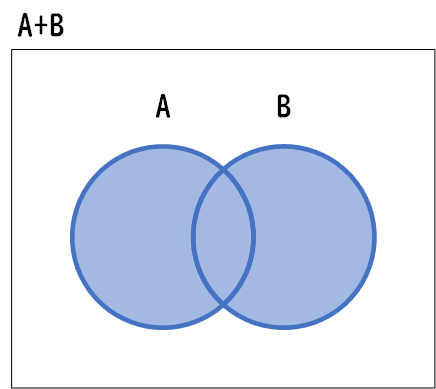
例えば、「A OR B」のベン図では、AとBの集合が重なる部分も含めた範囲が結果として表されます。
論理演算は、コンピューターやプログラミングなどで広く利用されており、条件分岐やデータ処理など様々な場面で活用されています。
検索エンジンの検索クエリ
GoogleやBingなどの検索エンジンでは、AND、OR、NOTといった論理演算を用いて検索クエリを細かく指定することができます。
たとえば、「iPhone AND review」を検索すると、iPhoneのレビューに関するページだけが結果として表示されます。同様に、「cats OR dogs」を検索すると、猫や犬に関するページが表示されます。さらに、「iPhone NOT review」を検索すると、iPhoneに関するページからレビューに関するページを除外した結果が表示されます。
オンラインショッピングのフィルタリング検索
オンラインショッピングサイトで商品を検索する際に、複数の条件を組み合わせて絞り込むことがあります。
たとえば、「男性向け」「Tシャツ」「価格が1000円以下」という条件にチェックを入れて商品を検索した場合、これらの条件を論理演算(AND)で組み合わせた結果が表示されます。
四種の論理演算
論理和 (OR)
論理和(OR)は、論理演算の一種で、2つの入力値(通常は真偽値)のうち少なくとも1つが真(True)であれば、結果も真(True)となる演算です。
「AまたはB」と表現し、論理演算記号では\(A + B\)または\(A \cup B\)という記号で表します。
論理和の真理値表は以下のようになります。
| A (入力) | B (入力) | A OR B (出力) |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
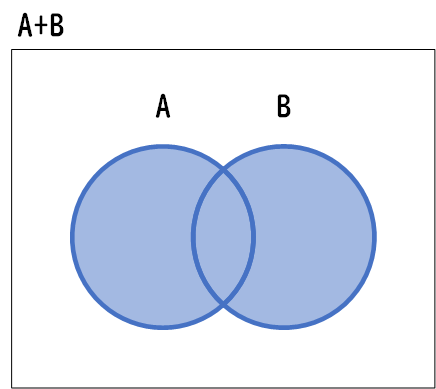
この真理値表は、入力Aと入力Bがどちらも偽(False)である場合にのみ、結果が偽(False)となり、それ以外のすべての組み合わせでは結果が真(True)であることを示しています。
勉強中眠たくなったときに、眠気覚ましにカフェインを取る場合
条件A:コーヒーを飲む。
条件B:紅茶を飲む。
条件Aまたは条件Bが真であれば、眠気を覚ますことができます。
論理積 (AND)
論理積(AND)は、論理演算の一種で、2つの入力値が両方とも真(1)である場合にのみ、結果が真(1)となる演算です。
「AかつB」と表現し、論理演算記号では\(A \cdot B\)または\(A \cap B\)という記号で表します。
論理積の真理値表は以下のようになります。ここでは、真を1、偽を0と表記しています。
| A (入力) | B (入力) | A AND B (出力) |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
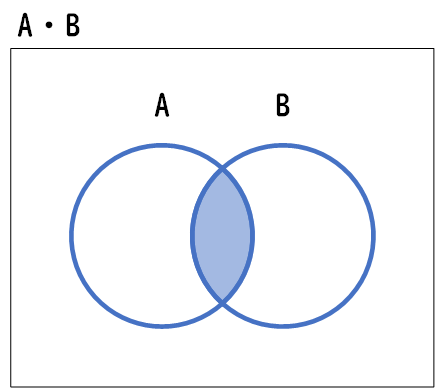
この真理値表は、入力Aと入力Bがどちらも真(1)である場合にのみ、結果が真(1)となり、それ以外のすべての組み合わせでは結果が偽(0)であることを示しています。
入試に合格するために、以下の条件を両方満たす必要がある大学があるとします。
・数学で60点以上
・英語で60点以上
この条件は論理積で表現できます。例えば、数学で65点かつ英語で70点ならば合格です。
一方これを満たさないケース、例えば、数学で50点・英語で40点、数学で40点・英語で90点、あるいは数学で80点・英語で55点などでは不合格となります。
否定 (NOT)
否定(NOT)は、論理演算の一種で、入力値が真(1)の場合は偽(0)を、偽(0)の場合は真(1)を返す演算です。
「Aではない」と表現し、論理演算記号では \(\overline{A}\) という記号で表します。
否定の真理値表は以下のようになります。ここでは、真を1、偽を0と表記しています。
| A (入力) | NOT A (出力) |
|---|---|
| 0 | 1 |
| 1 | 0 |
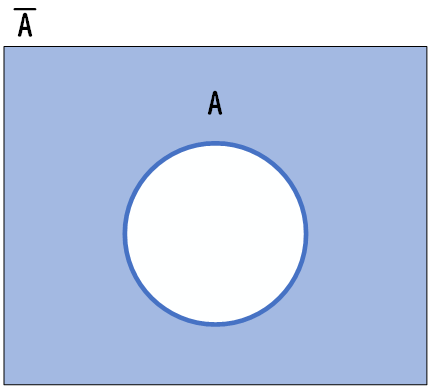
この真理値表は、入力Aが真(1)の場合、結果が偽(0)になり、入力Aが偽(0)の場合、結果が真(1)になることを示しています。
散歩好きなCさんが散歩に行くのは、雨が降っていない時だけです。
この場合、Cさんが散歩に行くためには、「NOT 雨が降っている」という条件を満たす必要があります。
排他的論理和 (XOR)
排他的論理和(XOR)は、論理演算の一種で、2つの入力値が異なる場合に真(1)を、同じ場合に偽(0)を返す演算です。
論理演算記号では \(A \oplus B\)という記号で表します。
排他的論理和の真理値表は以下のようになります。ここでは、真を1、偽を0と表記しています。
| A (入力) | B (入力) | A XOR B (出力) |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
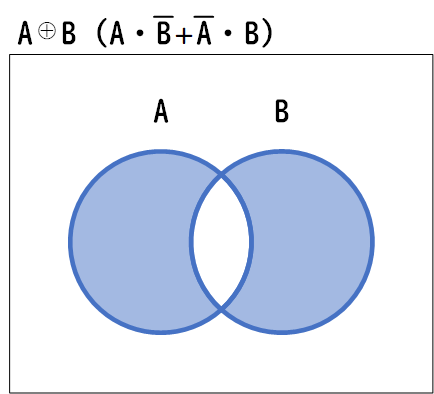
この真理値表は、入力Aと入力Bが異なる場合(0、1または1、0)、結果が真(1)になり、入力Aと入力Bが同じ場合(0、0または1、1)、結果が偽(0)になることを示しています。
いわゆる「二者択一」になる場合がXORに該当します。
例えば、レストランでメニューに「コーヒーまたは紅茶が付きます」と書かれていた場合、コーヒーと紅茶のどちらか一方のみが付くことを意味し、両方が付くことは意味しません。
