基数
基数とは、数を表すときの「一桁がいくつまで存在するか」を示す数のことです。
我々が日常的に用いる10進数では基数は「10」であり、これは一桁に0から9までの10種類の数字を使うことを意味します。
しかし、基数は10に限ったものではありません。コンピューターサイエンスでは、基数が2の2進数や16の16進数がよく使われます。
10進数と2進数・8進数・16進数
ここでは、よく使われる10進数・2進数・8進数・16進数の4種類について説明します。
10進数
10進数は、0から9までの10つの数字を用いて数値を表現します。人間が日常的に使用する数値表現であり、最も一般的な表記法です。
2進数
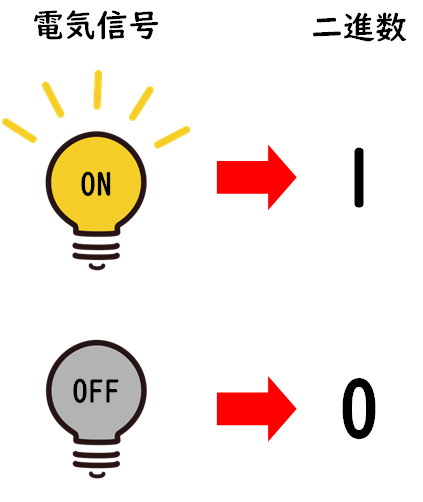
2進数は0と1の2種類の数字だけで数を表現します。
つまり、10進数の時に用いていた残りの2~9までの数字は使用しません。
コンピュータの世界では、電気信号のオン(1)とオフ(0)の状態を使用して情報を処理するため、2進数が使用されます。
ここで、コンピュータが処理する最小の単位、つまり2進数の1桁のことをビット(bit)と呼びます。
8進数
8進数は、0から7までの8つの数字を用いて数値を表現します。残りの8、9は使用しません。
8進数はコンピュータで2進数を扱うための一つの便利な方法です。
なぜなら、8進数1桁は2進数の3ビット分に対応するからです。
例えば、2進数の「101」は8進数で「5」になります。このように、8進数は長い2進数を短縮して人間が読みやすくするためによく用いられます。
16進数
16進数は、今までとは逆に0~9の10個の数字では足りないので、A(10)からF(15)までの6つの英字を追加で用いて表現します。
16進数も8進数と同様に、2進数の表現をより短縮し読みやすくするために使用されます。16進数1桁は2進数4ビット分に対応します。つまり、2進数の「1010」は16進数で「A」になります。
16進数はメモリアドレスやカラーコード(HTMLなど)の表現に使われることが多いです。
10進数と2進数・8進数・16進数の比較
並べて比較すると以下のようになります。赤い背景のセルで桁が上がっていることに注目してください。
| 10進数 | 2進数 | 8進数 | 16進数 |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 |
| 2 | 10 | 2 | 2 |
| 3 | 11 | 3 | 3 |
| 4 | 100 | 4 | 4 |
| 5 | 101 | 5 | 5 |
| 6 | 110 | 6 | 6 |
| 7 | 111 | 7 | 7 |
| 8 | 1000 | 10 | 8 |
| 9 | 1001 | 11 | 9 |
| 10 | 1010 | 12 | A |
| 11 | 1011 | 13 | B |
| 12 | 1100 | 14 | C |
| 13 | 1101 | 15 | D |
| 14 | 1110 | 16 | E |
| 15 | 1111 | 17 | F |
| 16 | 10000 | 20 | 10 |
基数と重み
重みとは、数値を表現する際に各桁がどの程度の価値を持つかを示す概念です。
10進数、2進数、16進数などの各進数において、右から左へ桁が上がるごとに基数のべき乗が増えていきます。これが各桁の重みを決定します。
例として、「123.456」という数の重みを、10進数と16進数の場合で比較してみましょう。
10進数の各桁の重み
10進数における「123.456」は、
\( \displaystyle {}1\times10^2+2\times10^1+3\times10^0+4\times10^{-1}+5\times10^{-2}+6\times10^{-3} \)
- 1の位の「重み」は100 = 1
- 10の位の「重み」は101 = 10
- 100の位の「重み」は102 = 100
また、小数点以下は
- 小数第一位の「重み」は10-1 = 0.1
- 小数第二位の「重み」は10-2 = 0.01
- 小数第三位の「重み」は10-3 = 0.001
16進数の各桁の重み
16進数における「123.456」は、
\( \displaystyle {}1\times16^2+2\times16^1+3\times16^0+4\times16^{-1}+5\times16^{-2}+6\times16^{-3} \)
- 1の位の「重み」は160 = 1
- 10の位の「重み」は161 = 16
- 100の位の「重み」は162 = 256
また、小数点以下は
- 小数第一位の「重み」は16-1 = 1/16 = 0.0625
- 小数第二位の「重み」は16-2 = 1/256 = 0.00390625
- 小数第三位の「重み」は16-3 = 1/4096 = 0.00024414…
以上を踏まえて、16進数での123.456の値を10進数に直すと、291.2709961…という値になります。
このように基数が異なると、各桁の重みが変わってくるため、同じ表記であっても異なる数値になることが分かります。
16進数は上記の例のようにアルファベットが含まれない場合、10進数と見分けがつかないことがあります。
このような場合、どう判別すればよいのでしょうか?
一般的なプログラミング言語では、16進数表記であることを区別するために、数値の頭に「0x」という表記を付け加えることがあります。
つまり、16進数の123.456は「0x123.456」と表記します。
各進数の重みを表にまとめると以下のようになります。
| 4桁目 | 3桁目 | 2桁目 | 1桁目 | 小数点 | 小数 第1位 | 小数 第2位 | 小数 第3位 | |
|---|---|---|---|---|---|---|---|---|
| 10進数 | 103 | 102 | 101 | 100 | . | 10-1 | 10-2 | 10-3 |
| 2進数 | 23 | 22 | 21 | 20 | . | 2-1 | 2-2 | 2-3 |
| 8進数 | 83 | 82 | 81 | 80 | . | 8-1 | 8-2 | 8-3 |
| 16進数 | 163 | 162 | 161 | 160 | . | 16-1 | 16-2 | 16-3 |
上記の表を10進数で表現すると以下のような表になります。
※「-」の部分はその進数で通常使用されません。
| 4桁目 | 3桁目 | 2桁目 | 1桁目 | 小数点 | 小数 第1位 | 小数 第2位 | 小数 第3位 | |
|---|---|---|---|---|---|---|---|---|
| 10進数 | 1000 | 100 | 10 | 1 | . | 0.1 | 0.01 | 0.001 |
| 2進数 | 8 | 4 | 2 | 1 | . | 0.5 | 0.25 | 0.125 |
| 8進数 | 512 | 64 | 8 | 1 | . | – | – | – |
| 16進数 | 4096 | 256 | 16 | 1 | . | – | – | – |
基数変換
基数変換とは、ある進数で表現された数値を別の進数で表現することです。
※余談ですが、以下の内容は高校数学でも学習します。これから学習する方は覚えておいて損はありません。
2進数から10進数への基数変換
2進数から10進数への基数変換は、2進数の各桁の重みを利用して計算します。
例えば、2進数の「1010.101」を10進数に変換する場合を考えてみましょう。
まず、以下の表のように、2進数の各桁の値と重みを掛け合わせます。
| 4桁目 | 3桁目 | 2桁目 | 1桁目 | 小数点 | 小数 第1位 | 小数 第2位 | 小数 第3位 | |
|---|---|---|---|---|---|---|---|---|
| 2進数 | 1 | 0 | 1 | 0 | . | 1 | 0 | 1 |
| × | × | × | × | × | × | × | ||
| 2進数の重み | 8 | 4 | 2 | 1 | . | 0.5 | 0.25 | 0.125 |
| ↓ | ↓ | ↓ | ↓ | ↓ | ↓ | ↓ | ||
| 2進数×重み | 8 | 0 | 2 | 0 | . | 0.5 | 0 | 0.125 |
掛け合わせた結果(8、0、2、0、0.5、0.125)を全て足し合わせると、「8 + 0 + 2 + 0 + 0.5 + 0.125 = 10.625」となります。よって2進数の「1010.101」は10進数で「10.625」と表現できます。
つまり、以下の2ステップで計算ができます。
- 各桁の数字と重みを掛ける
- それらを全て足し合わせる
このように、2進数から10進数への基数変換は、各桁の重みを利用して計算することで可能となります。
10進数から2進数への基数変換
今度は逆に10進数から2進数への基数変換を考えてみましょう。こちらは2通りの方法を説明します。
解法1
例えば、10進数の数値「58」を2進数に変換する場合、「すだれ算」を用いて計算します。以下のように商が0になるまで2で割ることを繰り返します。
\begin{array}{rcl}
2\!&\underline{)\,58} &\\
2\!&\underline{)\,29} &…0\\
2\!&\underline{)\,14} &…1\\
2\!&\underline{)\,\phantom{0}7} &…0\\
2\!&\underline{)\,\phantom{0}3} &…1\\
2\!&\underline{)\,\phantom{0}1} &…1\\
&\phantom{2\!\underline{)\,}}0 &…1\\
\end{array}
58÷2=29 余り0(以下、商が0になるまで割ることを続けます)
29÷2=14 余り1
14÷2= 7 余り0
7÷2= 3 余り1
3÷2= 1 余り1
1÷2= 0 余り1
これらの余りを下から並べると「111010」という58を2進数で表現した値が求まります。
同様に、8進数や16進数に変換する場合も、それぞれの進数で割り算を行い、余りを下から並べて求めることができます。
解法2
| 7桁目 | 6桁目 | 5桁目 | 4桁目 | 3桁目 | 2桁目 | 1桁目 | |
|---|---|---|---|---|---|---|---|
| 2進数 | 26 | 25 | 24 | 23 | 22 | 21 | 20 |
| 10進数 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
2進数と10進数の対応表を用いることでも、2進数への基数変換が行えます。先ほどと同様に「58」を2進数に変換してみましょう。
58は7桁目の64よりも小さいので7桁目は0にします。
58は次の6桁目の32より大きいので6桁目を1にします。余りは58-32=26。以下、この手順を繰り返します。
26は5桁目の16より大きいので5桁目を1にします。余りは26-16=10
10は4桁目の8より大きいので4桁目を1にします。余りは10-8=2
2は3桁目の4より小さいので3桁目を0にします。余りは2のまま。
2は2桁目の2と等しいので2桁目を1にします。余りは2-2=0
よって、58を2進数で表すと「111010」になります。
このように、2進数と10進数は相互に変換することができます。
よって、内部的に2進数を用いるコンピュータであっても、人間が理解しやすい10進数の形で処理結果を表示することができるのです。
2進数の筆算
2進数の筆算は10進数の筆算と同様に桁を縦にそろえて計算します。
10進数では足して10になると桁が上がりますが、2進数では足して2になると1つ桁が上がります。
ここでは、2進数の1111と101を足します。答えは以下の筆算を行い、10100と求めることができます。
\begin{array}{cccccc}
&&\small{1}&\small{1}&\small{1}\\
&&1 & 1& 1 & 1\\
+&&& 1 & 0 & 1\\
\hline
&1 & 0 & 1 & 0 & 0\\
\end{array}
