統計
統計における基本的な概念である平均値、メジアン、モード、レンジ、分散、標準偏差について説明します。
具体的な例として、次のデータセットを考えましょう。
3, 5, 2, 6, 2, 8, 6, 7, 2
平均値(Mean)
平均値は、データセット内の全ての数値を合計して、数値の総数で割った値です。
これはデータの「中心的な傾向」を示すもので、一般的に「平均」と呼ばれます。
平均値はデータセット全体を代表する値ですが、外れ値(極端に高い値や低い値)の影響を受けやすい点に注意が必要です。
\( \displaystyle {}\textbf{平均値} = \frac{3+5+2+6+2+8+6+7+2}{9} = 4.89 \)
中央値(Median:メジアン)
中央値は、データセットを小さい順に並べたときに、真ん中に位置する値です。
データの数が奇数の場合は、中央に位置する値そのものが中央値になります。データの数が偶数の場合は、中央に位置する2つの値の平均が中央値になります。
中央値は外れ値の影響を受けにくいため、データセットの「中心」を示すのに平均値より適している場合があります。
このデータセットを昇順に並べると 2, 2, 2, 3, 5, 6, 6, 7, 8 となり、中央値は中央の数値である5です。
モード(Mode:最頻値)
モード(最頻値)は、データセット内で最も頻繁に出現する値です。
データセットにおいて、最も一般的な値を示します。
データセットにはモードが1つだけの場合もあれば、複数のモードを持つこともあります。また、全ての値が同じ回数だけ出現する場合、モードは存在しないとされます。
このデータセットでは、2が最も頻繁に出現(3回)しているので、モードは2です。
レンジ(Range:範囲)
データセットの最大値と最小値の差です。
この数値は、データの散らばり具合を最も単純に示す指標であり、データセットの変動の幅を捉えます。
このデータセットの最大値は8、最小値は2なので、レンジは 8 – 2 = 6 となります。
分散(Variance)
分散はデータのばらつきを数値化する指標で、データがその平均値からどれだけ離れて分布しているかを示します。
具体的には、各データと平均値との差(偏差)を二乗したものの平均です。分散が大きいほど、データは平均値から広がっていると言えます。
\begin{flalign*}
& \text{分散} = \frac{\sum \left( \text{各データ} – \text{(平均)} \right)^2}{\text{全体の人数}} &
\end{flalign*}
\begin{flalign*}
& S^2 = \frac{1}{n} \sum_{i=1}^{n} (x_i – \overline{x})^2 &
\end{flalign*}
分散はデータの散らばり具合をより詳細に示すことができますが、単位が元のデータの二乗になるため、解釈が直感的でないことがあります。
このデータセットの分散は以下のようになります。
\( \displaystyle {}\textbf{分散} = \frac{(3-4.89)^2 + (5-4.89)^2 + (2-4.89)^2 + (6-4.89)^2 + (2-4.89)^2 + (8-4.89)^2 + (6-4.89)^2 + (7-4.89)^2 + (2-4.89)^2}{9} = 4.54\)
標準偏差(Standard Deviation)
標準偏差は分散の平方根であり、分散同様にデータのばらつきを示す指標です。
標準偏差は分散と同様にデータの平均値からの偏差を捉えますが、単位が元のデータと同じであるため、解釈しやすいという利点があります。標準偏差が大きいほど、データの散らばりが大きいことを意味します。
例えば、テストの点数が平均点から大きく離れているクラスは標準偏差が大きく、ほとんどの生徒の点数が平均点に近いクラスは標準偏差が小さくなります。
このデータセットの標準偏差は以下のようになります。
\( \displaystyle {}\textbf{標準偏差} = \sqrt{\textbf{分散}} = \sqrt{4.54} \fallingdotseq 2.13\)
分散と標準偏差は、データがどれだけ散らばっているか、つまりデータが平均値からどの程度離れているかを示す指標です。これらはデータの変動性や予測の信頼度を評価するために非常に重要です。
例えば、あるクラスの学生たちのテストのスコアを考えてみましょう。クラスAとクラスBの2つのクラスがあり、両クラスともテストの平均点が70点だったとします。
ただし、クラスAの学生のスコアはほとんどが68点から72点の間に集中しているのに対し、クラスBの学生のスコアは50点から90点まで幅広く分布しているとします。
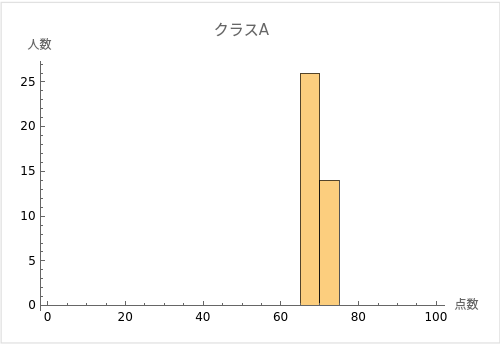
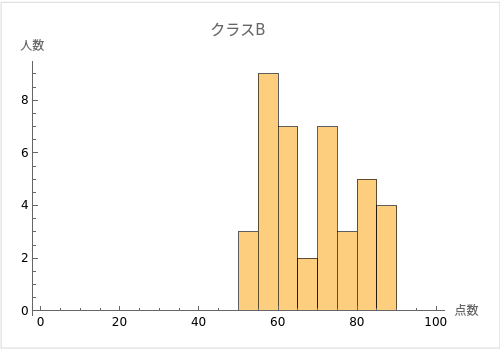
この場合、両クラスとも平均点は70点ですが、クラスAの学生のスコアは平均値の周囲に密集しており、クラスBの学生のスコアは平均値から大きく離れたところにも広がっていることが分かります。
つまり、クラスAのスコアの分散と標準偏差は小さく、クラスBのスコアの分散と標準偏差は大きいと言えます。
このように、分散と標準偏差はデータの散らばり具合を示すことで、データの特性をより詳しく理解することを可能にします。また、この情報はデータの予測や解釈、比較においても重要な役割を果たします。
正規分布
正規分布(ガウス分布とも呼ばれる)は、自然現象や社会現象におけるランダムなデータの分布を表すのによく用いられる統計的な分布の形です。
その形は鐘型で、平均値(μ)を中心に左右対称になっています。
正規分布の特徴は以下の通りです。
- データは平均値(μ)を中心に分布します。
- 平均値を中心にして、左右対称の形状を持ちます。
- 分布の標準偏差(σ)が大きいほど、データはより広範囲に分布します(つまり、分布は広がります)。
- 分布の標準偏差(σ)が小さいほど、データはより狭範囲に集中します(つまり、分布は尖ります)。
- すべての正規分布は同じ基本的な形状(鐘型)を持ちますが、平均値と標準偏差により形状や位置が異なります。
正規分布の例
人間の身長、テストのスコア、製品の寿命などは、一般的に正規分布に近い形を示します。
たとえば、大人の男性の平均身長が170cmで、標準偏差が10cmとしましょう。これは、大多数の男性の身長が160cmから180cmの間に集中し、非常に背の低いまたは高い男性(例えば、150cm以下または190cm以上)は少ないことを示します。
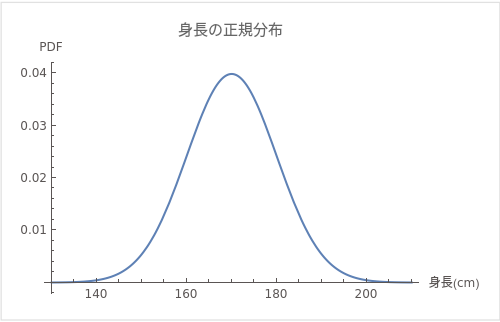
上図は平均身長が170cmで、標準偏差が10cmの正規分布のグラフです。x軸は身長(cm)を、y軸はその身長の確率密度関数(PDF)を示しています。
正規分布の用途
正規分布は日常生活やビジネスの中で多くの場面で役立ちます。具体的な例を以下に示します。
- テストの成績分析: 学生のテストスコアはしばしば正規分布に従います。平均スコア(平均)とスコアの分散(標準偏差)を知ることで、ある学生が全体の中でどの位置にいるかを評価することができます。例えば、あるテストの平均スコアが70で標準偏差が10だとします。スコアが80の生徒は、全体の中で平均よりも高い成績を収めています。
- 身体の特徴: 人々の身長や体重などは、通常、正規分布に従います。これは、大多数の人々が平均的な値周辺に位置し、極端に高い人や低い人が少ないという特性を反映しています。これは、新しい製品(例えば、衣類や家具)の設計時に非常に重要です。平均的な値を元に設計することで、最も多くの人々に適した製品を作ることができます。
- 品質管理: ある製品の製造過程で、製品の重量や寸法が正規分布に従っていると仮定できます。この分布を理解することで、製造プロセスが目標通りに機能しているか、または製造プロセスが不安定であることを示す異常値があるかを判断することができます。
- 金融投資: 正規分布は投資リスクの評価にも使用されます。特定の投資の収益率が正規分布に従っていると仮定すれば、その投資が将来どれだけの利益をもたらす可能性があり、またそのリスクはどれくらいかを評価することができます。
- 医療: 患者の体温、血圧、コレステロールレベルなどは通常、正規分布に従います。これは、医療専門家が健康状態を評価し、異常値を特定するのに役立ちます。例えば、平均体温が標準的な範囲から大きく逸脱していれば、それは病気や感染の可能性を示すかもしれません。
- 社会科学: 正規分布は意見調査や行動研究など、社会科学の多くの分野で用いられます。たとえば、ある都市の住民の意見を調査する際、回答はしばしば正規分布を形成します。これにより、大多数の人々がどのように感じているか、またはどの問題が最も関心を持たれているかを把握することができます。
以上のように、正規分布は自然科学や社会科学のさまざまな分野で用いられています。
関連用語
外れ値は、データ分布の中で他の値から大きく離れている値を指します。例えば、成績のデータで、大半の学生が70点から90点の間に分布しているにもかかわらず、一部の学生が10点または100点を取った場合、これらのスコアは外れ値となります。外れ値は常に問題を示すものではなく、有用な情報を提供することもあります。
異常値は、期待されるパターンから大きく逸脱したデータ点を指します。これはしばしばエラーや異常を示します。例えば、クレジットカードの取引で、一人のユーザーが通常の月平均取引額を大きく超える取引をした場合、この取引は異常値と見なされ、不正利用の可能性があります。異常値は大抵、問題を示しているため、発見と対処が必要です。
